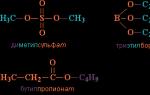
Агиляр эугенио мануэль фернандес. Песчинки во Вселенной

Уроженец греческого города Сиракузы на острове Сицилия, Архимед был приближенным управлявшего городом царя Гиерона (и, вероятно, его родственником). Возможно, какое-то время Архимед жил в Александрии – знаменитом научном центре того времени. То, что сообщения о своих открытиях он адресовал математикам, связанным с Александрией, например Эратосфену , подтверждает мнение о том, что Архимед являлся одним из деятельных преемников Евклида , развивавших математические традиции александрийской школы. Вернувшись в Сиракузы, Архимед находился там вплоть до своей гибели при захвате Сиракуз римлянами в 212 до н.э.

Дата рождения Архимеда (287 до н.э.) определяется исходя из свидетельства византийского историка 12 в. Иоанна Цеца, согласно которому он «прожил семьдесят пять лет». Яркие картины его гибели, описанные Ливием , Плутархом и Валерием Максимом, различаются лишь в деталях, но сходятся в том, что Архимеда, занимавшегося в глубокой задумчивости геометрическими построениями, зарубил римский воин. Кроме того, Плутарх сообщает, что Архимед, «как утверждают, завещал родным и друзьям установить на его могиле описанный вокруг шара цилиндр с указанием отношения объема описанного тела к вписанному», что было одним из наиболее славных его открытий. Цицерон, который в 75 до н.э. был на Сицилии, обнаружил выглядывавшее из колючего кустарника надгробие и на нем – шар и цилиндр.

Легенды об Архимеде.

В наше время имя Архимеда связывают главным образом с его замечательными математическими работами, однако в античности он прославился также как изобретатель различного рода механических устройств и инструментов, о чем сообщают авторы, жившие в более позднюю эпоху. Правда, авторство Архимеда во многих случаях вызывает сомнения. Так, считается, что Архимед был изобретателем т.н. архимедова винта, который служил для подъема воды на поля и явился прообразом корабельных и воздушных винтов, хотя, судя по всему, такого рода устройство использовалось и раньше. Не внушает особого доверия и то, что рассказывает Плутарх в Жизнеописании Марцелла . Здесь говорится, что в ответ на просьбу царя Гиерона продемонстрировать, как тяжелый груз может быть сдвинут малой силой, Архимед «взял трехмачтовое грузовое судно, которое перед этим с превеликим трудом вытянули на берег много людей, усадил на него множество народа и загрузил обычным грузом. После этого Архимед сел поодаль и стал без особых усилий тянуть на себя канат, перекинутый через полиспаст, отчего судно легко и плавно, словно по воде, «поплыло» к нему». Именно в связи с этой историей Плутарх приводит замечание Архимеда, что, «если бы имелась иная Земля, он сдвинул бы нашу, перейдя на ту» (более известный вариант этого высказывания сообщает Папп Александрийский: «Дайте мне, где стать, и я сдвину Землю»). Вызывает сомнение и подлинность истории, поведанной Витрувием, что будто бы царь Гиерон поручил Архимеду проверить, из чистого ли золота сделана его корона или же ювелир присвоил часть золота, сплавив его с серебром. «Размышляя над этой задачей, Архимед как-то зашел в баню и там, погрузившись в ванну, заметил, что количество воды, переливающейся через край, равно количеству воды, вытесненной его телом. Это наблюдение подсказало Архимеду решение задачи о короне, и он, не медля ни секунды, выскочил из ванны и, как был нагой, бросился домой, крича во весь голос о своем открытии: «Эврика! Эврика!» (греч. «Нашел! Нашел!»)».

Более достоверным представляется свидетельство Паппа, что Архимеду принадлежало сочинение Об изготовлении [небесной ] сферы , речь в котором шла, вероятно, о построении модели планетария, воспроизводившей видимые движения Солнца, Луны и планет, а также, возможно, звездного глобуса с изображением созвездий. Во всяком случае Цицерон сообщает, что тот и другой инструмент захватил в Сиракузах в качестве трофеев Марцелл. Наконец, Полибий, Ливий, Плутарх и Цец сообщают о грандиозных баллистических и иных машинах, построеннных Архимедом для отражения римлян.

Математические труды.

Сохранившиеся математические сочинения Архимеда можно разделить на три группы. Сочинения первой группы посвящены в основном доказательству теорем о площадях и объемах криволинейных фигур или тел. Сюда относятся трактаты О шаре и цилиндре , Об измерении круга , О коноидах и сфероидах , О спиралях и О квадратуре параболы . Вторую группу составляют работы по геометрическому анализу статических и гидростатических задач: О равновесии плоских фигур , О плавающих телах . К третьей группе можно отнести различные математические работы: О методе механического доказательства теорем , Исчисление песчинок , Задача о быках и сохранившийся лишь в отрывках Стомахион . Существует еще одна работа – Книга о предположениях (или Книга лемм ), сохранившаяся лишь в арабском переводе. Хотя она и приписывается Архимеду, в своем нынешнем виде она явно принадлежит другому автору (поскольку в тексте имеются ссылки на Архимеда), но, возможно, здесь приведены доказательства, восходящие к Архимеду. Несколько других работ, приписываемых Архимеду древнегреческими и арабскими математиками, утеряны.

Дошедшие до нас работы не сохранили своей первоначальной формы. Так, судя по всему, I книга трактата О равновесии плоских фигур является отрывком из более обширного сочинения Элементы механики ; кроме того, она заметно отличается от II книги, написанной явно позднее. Доказательство, упоминаемое Архимедом в сочинении О шаре и цилиндре , было утрачено ко 2 в. н.э. Работа Об измерении круга сильно отличается от первоначального варианта, и предложение II в ней скорее всего заимствовано из другого сочинения. Заглавие О квадратуре параболы вряд ли могло принадлежать самому Архимеду, так как в его время слово «парабола» еще не использовалось в качестве названия одного из конических сечений. Тексты таких сочинений, как О шаре и цилиндре и Об измерении круга , скорее всего, подвергались изменениям в процессе перевода с дорийско-сицилийского на аттический диалект.

При доказательстве теорем о площадях фигур и объемах тел, ограниченных кривыми линиями или поверхностями, Архимед постоянно использует метод, известный как «метод исчерпывания». Изобрел его, вероятно, Евдокс (расцвет деятельности ок. 370 до н.э.) – по крайней мере, так считал сам Архимед. К этому методу время от времени прибегает и Евклид в XII книге Начал . Доказательство с помощью метода исчерпывания, в сущности, представляет собой косвенное доказательство от противного. Иначе говоря, утверждение «А равно В» считается истинным в том случае, когда принятие противоположного утверждения, «А не равно В», ведет к противоречию. Основная идея метода исчерпывания заключается в том, что в фигуру, площадь или объем которой требуется найти, вписывают (или вокруг нее описывают, либо же вписывают и описывают одновременно) правильные фигуры. Площадь или объем вписанных или описанных фигур увеличивают или уменьшают до тех пор, пока разность между площадью или объемом, которые требуется найти, и площадью или объемом вписанной фигуры не становится меньше заданной величины. Пользуясь различными вариантами метода исчерпывания, Архимед смог доказать различные теоремы, эквивалентные в современной записи соотношениям S = 4p r 2 для площади поверхности шара, V = 4/3p r 3 для его объема, теореме о том, что площадь сегмента параболы равна 4/3 площади треугольника, имеющего те же оcнование и высоту, что и сегмент, а также многие другие интересные теоремы.

Ясно, что, используя метод исчерпывания (который является скорее методом доказательства, а не открытия новых соотношений), Архимед должен был располагать каким-то другим методом, позволяющим находить формулы, которые составляют содержание доказанных им теорем. Один из методов нахождения формул раскрывает его трактат О механическом методе доказательства теорем . В трактате излагается механический метод, при котором Архимед мысленно уравновешивал геометрические фигуры, как бы лежащие на чашах весов. Уравновесив фигуру с неизвестной площадью или объемом с фигурой с известной площадью или объемом, Архимед отмечал относительные расстояния от центров тяжести этих двух фигур до точки подвеса коромысла весов и по закону рычага находил требуемые площадь или объем, выражая их соответственно через площадь или объем известной фигуры. Одно из основных допущений, используемых в методе исчерпывания, состоит в том, что площадь рассматривается как сумма чрезвычайно большого множества плотно прилегающих друг к другу «материальных» прямых, а объем – как сумма плоских сечений, тоже плотно прилегающих друг к другу. Архимед считал, что его механический метод не имеет доказательной силы, но позволяет получить предварительный результат, который впоследствии может быть доказан более строгими геометрическими методами.

Хотя Архимед был в первую очередь геометром, он совершил ряд интересных экскурсов и в область численных расчетов, пусть примененные им методы и не вполне ясны. В предложении III сочинения Об измерении круга он установил, что число p меньше и больше . Из доказательства видно, что он располагал алгоритмом получения приближенных значений квадратных корней из больших чисел. Интересно отметить, что у него приведена и приближенная оценка числа , а именно: . В сочинении, известном под названием Исчисление песчинок , Архимед излагает оригинальную систему представления больших чисел, позволившую ему записать число , где само Р равно . Эта система потребовалась ему, чтобы сосчитать, сколько песчинок понадобилось бы, чтобы заполнить Вселенную.

В труде О спирали Архимед исследовал свойства т.н. архимедовой спирали, записал в полярных координатах характеристическое свойство точек спирали, дал построение касательной к этой спирали, а также определил ее площадь.

В истории физики Архимед известен как один из основоположников успешного применения геометрии к статике и гидростатике. В I книге сочинения О равновесии плоских фигур он приводит чисто геометрический вывод закона рычага. По сути, его доказательство основано на сведении общего случая рычага с плечами, обратно пропорциональными приложенным к ним силам, к частному случаю равноплечего рычага и равных сил. Все доказательство от начала и до конца пронизано идеей геометрической симметрии.

В своем сочинении О плавающих телах Архимед применяет аналогичный метод к решению задач гидростатики. Исходя из двух допущений, сформулированных на геометрическом языке, Архимед доказывает теоремы (предложения) относительно величины погруженной части тел и веса тел в жидкости как с большей, так и с меньшей плотностью, чем само тело. В предложении VII, где говорится о телах более плотных, чем жидкость, выражен т.н. закон Архимеда, согласно которому «всякое тело, погруженное в жидкость, теряет по сравнению со своим весом в воздухе столько, сколько весит вытесненная им жидкость». В книге II содержатся тонкие соображения относительно устойчивости плавающих сегментов параболоида.

Влияние Архимеда.

В отличие от Евклида, Архимеда вспоминали в античности лишь от случая к случаю. Если мы что-то знаем о его работах, то лишь благодаря тому интересу, который питали к ним в Константинополе в 6–9 в. Эвтокий, математик, родившийся в конце 5 в., прокомментировал по крайней мере три работы Архимеда, по-видимому, наиболее известные в то время: О шаре и цилиндре , Об измерении круга и О равновесии плоских фигур . Работы Архимеда и комментарии Эвтокия изучали и преподавали математики Анфимий из Тралл и Исидор из Милета, архитекторы собора св. Софии, возведенного в Константинополе в правление императора Юстиниана. Реформа преподавания математики, которую проводил в Константинополе в 9 в. Лев Фессалоникийский, по-видимому, способствовала собиранию работ Архимеда. Тогда же он стал известен мусульманским математикам. Теперь мы видим, что арабским авторам недоставало некоторых наиболее важных работ Архимеда, таких как О квадратуре параболы , О спиралях , О коноидах и сфероидах , Исчисление песчинок и О методе . Но в целом арабы овладели методами, изложенными в других работах Архимеда, и нередко блестяще ими пользовались.

Средневековые латиноязычные ученые впервые услышали об Архимеде в 12 в., когда появились два перевода с арабского на латынь его сочинения Об измерении круга . Лучший перевод принадлежал знаменитому переводчику Герарду Кремонскому, и в последующие три столетия он послужил основой многих изложений и расширенных версий. Герарду принадлежал также перевод трактата Слова сынов Моисеевых арабского математика 9 в. Бану Мусы, в котором приводились теоремы из сочинения Архимеда О шаре и цилиндре с доказательством, аналогичным приведенному у Архимеда. В начале 13 в. Иоанн де Тинемюэ перевел сочинение О криволинейных поверхностях , по которому видно, что автор был знаком с другой работой Архимеда – О шаре и цилиндре . В 1269 доминиканец Вильгельм из Мербеке перевел с древнегреческого весь корпус работ Архимеда, кроме Исчисления песчинок , Метода и небольших сочинений Задача о быках и Стомахион . Для перевода Вильгельм из Мербеке использовал две из трех известных нам византийских рукописей (рукописи А и В). Мы можем проследить историю всех трех. Первая из них (рукопись А), источник всех копий, снятых в эпоху Возрождения, по-видимому, была утрачена примерно в 1544. Вторая рукопись (рукопись В), содержавшая работы Архимеда по механике, в том числе сочинение О плавающих телах , исчезла в 14 в. Копий с нее снято не было. Третья рукопись (рукопись С) не была известна до 1899, а изучать ее стали лишь с 1906. Именно рукопись С стала драгоценной находкой, так как содержала великолепное сочинение О методе , известное ранее лишь по отрывочным фрагментам, и древнегреческий текст О плавающих телах , исчезнувший после утраты в 14 в. рукописи В, которую использовал при переводе на латынь Вильгельм из Мербеке. Этот перевод имел хождение в 14 в. в Париже. Он использовался также Якобом Кремонским, когда в середине 15 в. тот предпринял новый перевод корпуса сочинений Архимеда, входивших в рукопись А (т.е. за исключением сочинения О плавающих телах ). Именно этот перевод, несколько поправленный Региомонтаном, был опубликован в 1644 в первом греческом издании трудов Архимеда, хотя некоторые переводы Вильгельма из Мербеке были изданы в 1501 и 1543. После 1544 известность Архимеда начала возрастать, и его методы оказали значительное влияние на таких ученых, как Симон Стевин и Галилей , а тем самым, хотя и косвенно, воздействовали на формирование современной механики.

АРХИМЕД (ок. 287-212 до н.э.), величайший древнегреческий математик и механик.

Жизнь.

Уроженец греческого города Сиракузы на острове Сицилия, Архимед был приближенным управлявшего городом царя Гиерона (и, вероятно, его родственником). Возможно, какое-то время Архимед жил в Александрии - знаменитом научном центре того времени. То, что сообщения о своих открытиях он адресовал математикам, связанным с Александрией, например Эратосфену , подтверждает мнение о том, что Архимед являлся одним из деятельных преемников Евклида , развивавших математические традиции александрийской школы. Вернувшись в Сиракузы, Архимед находился там вплоть до своей гибели при захвате Сиракуз римлянами в 212 до н.э.

Дата рождения Архимеда (287 до н.э.) определяется исходя из свидетельства византийского историка 12 в. Иоанна Цеца, согласно которому он «прожил семьдесят пять лет». Яркие картины его гибели, описанные Ливием , Плутархом и Валерием Максимом, различаются лишь в деталях, но сходятся в том, что Архимеда, занимавшегося в глубокой задумчивости геометрическими построениями, зарубил римский воин. Кроме того, Плутарх сообщает, что Архимед, «как утверждают, завещал родным и друзьям установить на его могиле описанный вокруг шара цилиндр с указанием отношения объема описанного тела к вписанному», что было одним из наиболее славных его открытий. Цицерон, который в 75 до н.э. был на Сицилии, обнаружил выглядывавшее из колючего кустарника надгробие и на нем - шар и цилиндр.

Убийство Архимеда Римлянином.

Легенды об Архимеде.

В наше время имя Архимеда связывают главным образом с его замечательными математическими работами, однако в античности он прославился также как изобретатель различного рода механических устройств и инструментов, о чем сообщают авторы, жившие в более позднюю эпоху. Правда, авторство Архимеда во многих случаях вызывает сомнения. Так, считается, что Архимед был изобретателем т.н. архимедова винта, который служил для подъема воды на поля и явился прообразом корабельных и воздушных винтов, хотя, судя по всему, такого рода устройство использовалось и раньше. Не внушает особого доверия и то, что рассказывает Плутарх в Жизнеописании Марцелла . Здесь говорится, что в ответ на просьбу царя Гиерона продемонстрировать, как тяжелый груз может быть сдвинут малой силой, Архимед «взял трехмачтовое грузовое судно, которое перед этим с превеликим трудом вытянули на берег много людей, усадил на него множество народа и загрузил обычным грузом. После этого Архимед сел поодаль и стал без особых усилий тянуть на себя канат, перекинутый через полиспаст, отчего судно легко и плавно, словно по воде, «поплыло» к нему». Именно в связи с этой историей Плутарх приводит замечание Архимеда, что, «если бы имелась иная Земля, он сдвинул бы нашу, перейдя на ту» (более известный вариант этого высказывания сообщает Папп Александрийский: «Дайте мне, где стать, и я сдвину Землю»). Вызывает сомнение и подлинность истории, поведанной Витрувием, что будто бы царь Гиерон поручил Архимеду проверить, из чистого ли золота сделана его корона или же ювелир присвоил часть золота, сплавив его с серебром. «Размышляя над этой задачей, Архимед как-то зашел в баню и там, погрузившись в ванну, заметил, что количество воды, переливающейся через край, равно количеству воды, вытесненной его телом. Это наблюдение подсказало Архимеду решение задачи о короне, и он, не медля ни секунды, выскочил из ванны и, как был нагой, бросился домой, крича во весь голос о своем открытии: «Эврика! Эврика!» (греч. «Нашел! Нашел!»)».

Более достоверным представляется свидетельство Паппа, что Архимеду принадлежало сочинение Об изготовлении [небесной ] сферы , речь в котором шла, вероятно, о построении модели планетария, воспроизводившей видимые движения Солнца, Луны и планет, а также, возможно, звездного глобуса с изображением созвездий. Во всяком случае Цицерон сообщает, что тот и другой инструмент захватил в Сиракузах в качестве трофеев Марцелл. Наконец, Полибий, Ливий, Плутарх и Цец сообщают о грандиозных баллистических и иных машинах, построеннных Архимедом для отражения римлян.

Математические труды.

Сохранившиеся математические сочинения Архимеда можно разделить на три группы. Сочинения первой группы посвящены в основном доказательству теорем о площадях и объемах криволинейных фигур или тел. Сюда относятся трактаты О шаре и цилиндре , Об измерении круга , О коноидах и сфероидах , О спиралях и О квадратуре параболы . Вторую группу составляют работы по геометрическому анализу статических и гидростатических задач: О равновесии плоских фигур , О плавающих телах . К третьей группе можно отнести различные математические работы: О методе механического доказательства теорем , Исчисление песчинок , Задача о быках и сохранившийся лишь в отрывках Стомахион . Существует еще одна работа - Книга о предположениях (или Книга лемм ), сохранившаяся лишь в арабском переводе. Хотя она и приписывается Архимеду, в своем нынешнем виде она явно принадлежит другому автору (поскольку в тексте имеются ссылки на Архимеда), но, возможно, здесь приведены доказательства, восходящие к Архимеду. Несколько других работ, приписываемых Архимеду древнегреческими и арабскими математиками, утеряны.

Дошедшие до нас работы не сохранили своей первоначальной формы. Так, судя по всему, I книга трактата О равновесии плоских фигур является отрывком из более обширного сочинения Элементы механики ; кроме того, она заметно отличается от II книги, написанной явно позднее. Доказательство, упоминаемое Архимедом в сочинении О шаре и цилиндре , было утрачено ко 2 в. н.э. Работа Об измерении круга сильно отличается от первоначального варианта, и предложение II в ней скорее всего заимствовано из другого сочинения. Заглавие О квадратуре параболы вряд ли могло принадлежать самому Архимеду, так как в его время слово «парабола» еще не использовалось в качестве названия одного из конических сечений. Тексты таких сочинений, как О шаре и цилиндре и Об измерении круга , скорее всего, подвергались изменениям в процессе перевода с дорийско-сицилийского на аттический диалект.

При доказательстве теорем о площадях фигур и объемах тел, ограниченных кривыми линиями или поверхностями, Архимед постоянно использует метод, известный как «метод исчерпывания». Изобрел его, вероятно, Евдокс (расцвет деятельности ок. 370 до н.э.) - по крайней мере, так считал сам Архимед. К этому методу время от времени прибегает и Евклид в XII книге Начал . Доказательство с помощью метода исчерпывания, в сущности, представляет собой косвенное доказательство от противного. Иначе говоря, утверждение «А равно В» считается истинным в том случае, когда принятие противоположного утверждения, «А не равно В», ведет к противоречию. Основная идея метода исчерпывания заключается в том, что в фигуру, площадь или объем которой требуется найти, вписывают (или вокруг нее описывают, либо же вписывают и описывают одновременно) правильные фигуры. Площадь или объем вписанных или описанных фигур увеличивают или уменьшают до тех пор, пока разность между площадью или объемом, которые требуется найти, и площадью или объемом вписанной фигуры не становится меньше заданной величины. Пользуясь различными вариантами метода исчерпывания, Архимед смог доказать различные теоремы, эквивалентные в современной записи соотношениям S = 4p r 2 для площади поверхности шара, V = 4/3p r 3 для его объема, теореме о том, что площадь сегмента параболы равна 4/3 площади треугольника, имеющего те же оcнование и высоту, что и сегмент, а также многие другие интересные теоремы.

Ясно, что, используя метод исчерпывания (который является скорее методом доказательства, а не открытия новых соотношений), Архимед должен был располагать каким-то другим методом, позволяющим находить формулы, которые составляют содержание доказанных им теорем. Один из методов нахождения формул раскрывает его трактат О механическом методе доказательства теорем . В трактате излагается механический метод, при котором Архимед мысленно уравновешивал геометрические фигуры, как бы лежащие на чашах весов. Уравновесив фигуру с неизвестной площадью или объемом с фигурой с известной площадью или объемом, Архимед отмечал относительные расстояния от центров тяжести этих двух фигур до точки подвеса коромысла весов и по закону рычага находил требуемые площадь или объем, выражая их соответственно через площадь или объем известной фигуры. Одно из основных допущений, используемых в методе исчерпывания, состоит в том, что площадь рассматривается как сумма чрезвычайно большого множества плотно прилегающих друг к другу «материальных» прямых, а объем - как сумма плоских сечений, тоже плотно прилегающих друг к другу. Архимед считал, что его механический метод не имеет доказательной силы, но позволяет получить предварительный результат, который впоследствии может быть доказан более строгими геометрическими методами.

Хотя Архимед был в первую очередь геометром, он совершил ряд интересных экскурсов и в область численных расчетов, пусть примененные им методы и не вполне ясны. В предложении III сочинения Об измерении круга он установил, что число p меньше и больше . Из доказательства видно, что он располагал алгоритмом получения приближенных значений квадратных корней из больших чисел. Интересно отметить, что у него приведена и приближенная оценка числа , а именно: . В сочинении, известном под названием Исчисление песчинок , Архимед излагает оригинальную систему представления больших чисел, позволившую ему записать число , где само Р равно . Эта система потребовалась ему, чтобы сосчитать, сколько песчинок понадобилось бы, чтобы заполнить Вселенную.

В труде О спирали Архимед исследовал свойства т.н. архимедовой спирали, записал в полярных координатах характеристическое свойство точек спирали, дал построение касательной к этой спирали, а также определил ее площадь.

В истории физики Архимед известен как один из основоположников успешного применения геометрии к статике и гидростатике. В I книге сочинения О равновесии плоских фигур он приводит чисто геометрический вывод закона рычага. По сути, его доказательство основано на сведении общего случая рычага с плечами, обратно пропорциональными приложенным к ним силам, к частному случаю равноплечего рычага и равных сил. Все доказательство от начала и до конца пронизано идеей геометрической симметрии.

В своем сочинении О плавающих телах Архимед применяет аналогичный метод к решению задач гидростатики. Исходя из двух допущений, сформулированных на геометрическом языке, Архимед доказывает теоремы (предложения) относительно величины погруженной части тел и веса тел в жидкости как с большей, так и с меньшей плотностью, чем само тело. В предложении VII, где говорится о телах более плотных, чем жидкость, выражен т.н. закон Архимеда, согласно которому «всякое тело, погруженное в жидкость, теряет по сравнению со своим весом в воздухе столько, сколько весит вытесненная им жидкость». В книге II содержатся тонкие соображения относительно устойчивости плавающих сегментов параболоида.

Влияние Архимеда.

В отличие от Евклида, Архимеда вспоминали в античности лишь от случая к случаю. Если мы что-то знаем о его работах, то лишь благодаря тому интересу, который питали к ним в Константинополе в 6-9 в. Эвтокий, математик, родившийся в конце 5 в., прокомментировал по крайней мере три работы Архимеда, по-видимому, наиболее известные в то время: О шаре и цилиндре , Об измерении круга и О равновесии плоских фигур . Работы Архимеда и комментарии Эвтокия изучали и преподавали математики Анфимий из Тралл и Исидор из Милета, архитекторы собора св. Софии, возведенного в Константинополе в правление императора Юстиниана. Реформа преподавания математики, которую проводил в Константинополе в 9 в. Лев Фессалоникийский, по-видимому, способствовала собиранию работ Архимеда. Тогда же он стал известен мусульманским математикам. Теперь мы видим, что арабским авторам недоставало некоторых наиболее важных работ Архимеда, таких как О квадратуре параболы , О спиралях , О коноидах и сфероидах , Исчисление песчинок и О методе . Но в целом арабы овладели методами, изложенными в других работах Архимеда, и нередко блестяще ими пользовались.

Средневековые латиноязычные ученые впервые услышали об Архимеде в 12 в., когда появились два перевода с арабского на латынь его сочинения Об измерении круга . Лучший перевод принадлежал знаменитому переводчику Герарду Кремонскому, и в последующие три столетия он послужил основой многих изложений и расширенных версий. Герарду принадлежал также перевод трактата Слова сынов Моисеевых арабского математика 9 в. Бану Мусы, в котором приводились теоремы из сочинения Архимеда О шаре и цилиндре с доказательством, аналогичным приведенному у Архимеда. В начале 13 в. Иоанн де Тинемюэ перевел сочинение О криволинейных поверхностях , по которому видно, что автор был знаком с другой работой Архимеда - О шаре и цилиндре . В 1269 доминиканец Вильгельм из Мербеке перевел с древнегреческого весь корпус работ Архимеда, кроме Исчисления песчинок , Метода и небольших сочинений Задача о быках и Стомахион . Для перевода Вильгельм из Мербеке использовал две из трех известных нам византийских рукописей (рукописи А и В). Мы можем проследить историю всех трех. Первая из них (рукопись А), источник всех копий, снятых в эпоху Возрождения, по-видимому, была утрачена примерно в 1544. Вторая рукопись (рукопись В), содержавшая работы Архимеда по механике, в том числе сочинение О плавающих телах , исчезла в 14 в. Копий с нее снято не было. Третья рукопись (рукопись С) не была известна до 1899, а изучать ее стали лишь с 1906. Именно рукопись С стала драгоценной находкой, так как содержала великолепное сочинение О методе , известное ранее лишь по отрывочным фрагментам, и древнегреческий текст О плавающих телах , исчезнувший после утраты в 14 в. рукописи В, которую использовал при переводе на латынь Вильгельм из Мербеке. Этот перевод имел хождение в 14 в. в Париже. Он использовался также Якобом Кремонским, когда в середине 15 в. тот предпринял новый перевод корпуса сочинений Архимеда, входивших в рукопись А (т.е. за исключением сочинения О плавающих телах ). Именно этот перевод, несколько поправленный Региомонтаном, был опубликован в 1644 в первом греческом издании трудов Архимеда, хотя некоторые переводы Вильгельма из Мербеке были изданы в 1501 и 1543. После 1544 известность Архимеда начала возрастать, и его методы оказали значительное влияние на таких ученых, как Симон Стевин и Галилей , а тем самым, хотя и косвенно, воздействовали на формирование современной механики.

Сергей Житомирский

Архимед-физик

Архимеда справедливо считают основоположником математической физики. С его именем связывается введение понятия центра тяжести, открытие законов рычага и разработка основ гидростатики. Известно, что он занимался и геометрической оптикой, хотя его работы в этой области до нас не дошли. Для древних греков физика была целостным учением о мире и считалась частью философии. Ее практические стороны, такие, как механика, относились к прикладным дисциплинам. Математика хотя и применялась, но от нее не требовали ни строгости, ни полноты описания явлений.

Архимед первым подошел к решению физических задач с широким применением математики. Как уже говорилось, он начал с механики. Античные механические представления настолько отличались от наших, что сейчас воспринимаются с трудом, хотя «Физику» Аристотеля (384...322 г. до н.э.) в течение многих столетий изучали, комментировали, считали безошибочной. Аристотель разделял движения на «естественные» и «насильственные». Естественным считалось стремление материи к своему «месту», зависящему от ее свойств, например стремление камня к центру; Земли, огня – от Земли вверх. Насильственные движения предполагали внешнюю причину – приложение силы. Механика Аристотеля не знала явления инерции: движение должно было прекратиться тотчас же после прекращения действия силы. Движение же по инерции объяснялось влиянием среды. Так, последователи Аристотеля считали, что при бросании камня возникает воздушный вихрь, несущий его после того, как камень покинул руку.

В своих трудах Архимед изучал только силы, которые с точки зрения аристотелевой механики вызывают «естественные» движения. Более того, он сразу упростил задачу, исключив из нее движение. Так появилась статика.

До Архимеда закон рычага рассматривался в сочинении «Механические проблемы», автором которого долгое время считался Аристотель.

В «Механических проблемах», которые составлены в форме вопросов и ответов, содержится описание ряда инструментов и механизмов (рычаг, колодезный журавль с противовесом, клещи, кривошип, полиспаст, зубчатые колеса, рычажные весы) и объяснение их действия на основе «принципа рычага» и правила: «Выигрываем в скорости (пути) – проигрываем в силе».

Однако отсутствие ясности в постановке задач в ряде случаев приводило к совершенно неправильным представлениям. Вот как, например, описывается в «Проблемах» работа корабельного руля: «Почему малый руль, привешенный на корме корабля, имеет столь большую силу?.. Быть может, потому, что руль есть рычаг, а рулевой есть то, что приводит его в действие? Стало быть, место, где он прикреплен к кораблю, становится точкой опоры, руль в целом – рычагом, море – грузом, а рулевой – движущей силой». Действие руля, основанное на силе реакции отталкиваемой им воды, разумеется, нельзя свести к простому рычагу.

Нечетким рассуждениям, содержавшимся в «Механических проблемах», Архимед противопоставил безупречную теорию, построенную по законам геометрии. Архимед сделал в механике то, что греческие геометры сделали в египетской и вавилонской землемерной науке. Вместо полей они рассматривали отрезки плоскостей, вместо межевых границ – бесконечно тонкие и абсолютно прямые (или имеющие строго обусловленную кривизну) линии. И тогда оказалось возможным найти между фигурами соотношения, о которых не подозревала восточная математика, удовлетворявшаяся решением практических задач.

Архимед придал геометрическим фигурам вес, равномерно распределенный по площади или объему. В отличие от автора «Механических проблем» он рассматривает не реальные рычаги или барабаны, а их идеализированные схемы. Это тем более замечательно, что Архимед был и блестящим практиком-конструктором.

Из механических, вернее, механогеометрических сочинений Архимеда до нас дошли только два: «О равновесии плоских фигур» и «Эфод, или послание Эратосфену о механических теоремах». Однако отрывки из его более ранних механических сочинений «О весах» и «О рычагах» сохранились в произведениях ряда авторов. Наиболее важные из них, относящиеся к учению о центре тяжести, имеются в «Механике» александрийского ученого I в. н.э. Герона и в «Математической библиотеке» ученого III в. н.э. (также александрийца) Паппа.

Центр тяжести

Первым открытием Архимеда в механике было введение понятия центра тяжести, т.е. доказательство того, что в любом теле есть единственная точка, в которой можно сосредоточить его вес, не нарушив равновесного состояния.

Герон и Папп приводят со ссылкой на Архимеда доказательство существования центра тяжести. Герон предваряет теорему фразой, относящейся к рассмотрению Архимедом идеализированных «физико-математических» тел (метод абстракции). Герон пишет: «Никто не отрицает, что о наклонении и отклонении в действительности говорят только о телах. Если же мы говорим о плоских или телесных (объемных) фигурах, что некоторая точка является их центром поворота и центром тяжести, то это достаточно разъяснено Архимедом». Эта фраза подтверждает, что замена тел их теоретическими моделями была в науке новшеством, введенным Архимедом.

Архимедовы определение центра тяжести и теорему о его существовании мы приведем в пересказе Паппа.

Определение центра тяжести формулируется так: «...центром тяжести некоторого тела является некоторая расположенная внутри него точка, обладающая тем свойством, что если за нее мысленно подвесить тяжелое тело, то оно останется в покое и сохранит первоначальное положение».

Доказательство существования центра тяжести также основано на мысленном уравновешивании тела. В нем тело мысленно помещают на горизонтальную прямую, являющуюся основанием вертикальной плоскости (рис. 1): «Если какое-нибудь обладающее весом тело положить на прямую CD так, чтобы оно полностью рассекалось продолжением упомянутой плоскости, то оно может иногда занять такое положение, что будет оставаться в покое... Если затем переставить груз так, чтобы он касался прямой CD другой своей частью, то можно при поворачивании дать ему такое положение, что он, будучи отпущен, останется в покое... Если снова вообразить плоскость ABCD продолженной, то она разделит груз на две взаимно уравновешивающиеся части и пересечется с первой плоскостью... Если бы эти плоскости не пересеклись, то те же самые части были бы и уравновешивающимися и неуравновешивающимися, что нелепо».

Рис. 1. К определению центра тяжести тела

Действительно, если бы плоскости, рассекающие груз на уравновешенные части, оказались параллельными (не пересекались), то можно было бы уравновесить тело, не поворачивая его, а только сдвинув параллельно самому себе. Это означало бы, что к одной из частей добавился бы отнятый от второй части объем, заключенный между плоскостями, что должно было бы нарушить равновесие. Путем подобных же рассуждений доказывается, что на линии пересечения плоскостей находится единственная точка, являющаяся центром тяжести.

Архимед решил ряд задач на нахождение центров тяжести различных геометрических фигур: треугольника, параллелограмма, конуса, сегмента параболы.

Закон рычага

Закон рычага, вероятно, был сформулирован в одном из упомянутых выше не дошедших до нас сочинений Архимеда. Причем сохранившийся в «Механике» Герона отрывок из сочинения Архимеда показывает, что в этом сочинении рассматривался случай, когда точки приложения сил расположены на окружностях разного диаметра, имеющих общую точку поворота. Это схема таких механизмов, как ворот, зубчатая передача и амфирион (разновидность ворота, состоящая из сидящих на одном валу барабанов разного диаметра). Приведя теорему, сводящую этот случай к рычагу, Герон пишет: «Это доказал Архимед в своей книге о равновесии. Отсюда ясно, что можно сдвинуть большую величину малой силой».

Но более серьезную разработку этих проблем Архимед предпринял позже в сочинении «О равновесии плоских фигур», состоящем из двух частей. В первой приводится ряд аксиом и теорем общего характера, а во второй с их помощью решается задача о нахождении центра тяжести сегмента параболы. В этой работе Архимед впервые развил аксиоматический подход к механике. Он строит свою теорию на базе геометрии путем добавления к геометрическим аксиомам нескольких «механических» аксиом. Книга начинается так:

«Сделаем следующие допущения:

1. Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине.
2. Если при равновесии тяжестей на каких-нибудь длинах к одной из тяжестей будет что-нибудь прибавлено, то они не будут уравновешиваться, но перевесит та тяжесть, к которой будет прибавлено».

Архимед приводит семь аксиом и на их основании доказывает ряд теорем, касающихся определения общего центра тяжести двух или нескольких фигур. Нахождение общего центра тяжести фигур сводится к их уравновешиванию на воображаемом рычаге, поскольку такое уравновешивание произойдет, если точка подвеса окажется в этом центре.

1. «Соизмеримые величины уравновешиваются на длинах, которые будут обратно пропорциональны тяжестям».
2. «Если величины несоизмеримы, то они точно так же уравновешиваются на длинах, которые обратно пропорциональны этим величинам».

Разумеется, для практики, когда требуются лишь приближенные расчеты, вторая теорема не нужна. Но она имеет глубокий теоретический смысл, показывая, что закон рычага действует при любых отношениях плеч, включая и иррациональные.

Архимед не только ввел в геометрию новый класс задач (определение центров тяжести фигур), но и впервые применил при их решении «механические» методы (например, мысленное взвешивание для нахождения площадей сложных фигур).

Применив математику для изучения механического равновесия, Архимед показал, что математический подход к решению физических проблем не только помогает проникнуть в суть законов природы, но обогащает и саму математику.

«То механическое открытие»

В XI главе «Математической библиотеки» Паппа говорится: «Как определенный груз привести в движение определенной силой – это то механическое открытие Архимеда, которое заставило его радостно воскликнуть: «Дай мне место, где бы я мог стоять, и я подниму Землю!» Сходный по содержанию текст имеется у Плутарха, который рассказывает: «Архимед, между прочим, писал однажды своему родственнику и другу царю Гиерону, что данной силой можно поднять любую тяжесть. В юношески смелом доверии к силе своего доказательства он сказал, что, если бы у него была другая Земля, он перешел бы на нее и сдвинул с места нашу. Удивленный Гиерон стал просить его доказать свои слова и привести в движение какое-либо большое тело малой силой. Архимед приказал посадить на царскую грузовую триеру, с громадным трудом с помощью многих рук вытащенную на берег, большой экипаж, положить на нее обыкновенный груз и, усевшись на некотором расстоянии, без всяких усилий, спокойно двигая рукой конец полиспаста, стал тянуть к себе триеру так тихо и ровно, как будто она плыла по морю».

Таким образом, открытие связывается с эффектной механической демонстрацией и со знаменитой фразой Архимеда о том, что он смог бы сдвинуть саму Землю. Обычно эту фразу относят к открытию закона рычага. Но рычаг был известен с незапамятных времен, а закон его действия, хотя и не строго, уже был сформулирован в «Механических проблемах». Кроме того, при попытке сдвинуть рычагом очень большой груз, мы получим весьма малое перемещение. Также мало вероятно, чтобы эта фраза относилась к какому-нибудь изобретенному Архимедом механизму, например винту. Ведь Папп говорит о каком-то открытом Архимедом законе, «как определенный груз привести в движение определенной силой». Ссылаясь на книгу Герона «Барулк», Папп пишет: «В «Барулк» он описывает, как поднять определенный груз определенной силой, причем он принимает отношение диаметра колеса к диаметру оси равным 5:1, предварительно допустив, что подлежащий поднятию груз весит 1000 талантов (25 т), а движущая сила равна 5 талантам (125 кг)». Далее Папп, меняя условия задачи (поднять груз в 160 талантов силой 4 таланта), описывает расчет многоступенчатого зубчатого редуктора, имеющего на входе червячную передачу.Слово «барулк», видимо, и является названием описываемого механизма.

«Открытие» не названо, но по крайней мере теперь мы знаем, что оно заключено в механизме, который мы бы назвали лебедкой, содержащей барабан для наматывания каната, несколько зубчатых передач и червячную пару. Кроме червячной передачи, которая входит в состав лебедки, остальные механизмы – ворот и зубчатые колеса – упоминаются в «Механических проблемах» и, значит, были известны до Архимеда.

Новым здесь был сам принцип построения многоступенчатой передачи. Открытие Архимеда должно было состоять в нахождении закона определения общего «выигрыша в силе», достигаемого с помощью механизма, состоящего из последовательно соединенных передач. Этот закон можно сформулировать так: общее передаточное отношение многозвенного механизма равно произведению передаточных отношений его звеньев.

Но это простое правило приводит к ошеломляющим результатам. Если взять пару зубчатых колес с отношениями радиусов 1:5 (как у Герона), то получим на большом колесе «выигрыш в силе» в 5 раз. Если же мы на вал с малым колесом насадим еще одно такое же большое и сцепим его с еще одним таким же маленьким, то получится уже «выигрыш» в 25 раз. Для редуктора с тремя такими передачами он будет равен 125, с пятью – 3125, а с семью передачами составит 390 625; наконец, взяв всего 12 передач, получим астрономическое число 1 220 703 125!

Найдя этот закон, Архимед открыл, на что способна механика, и счел не лишним продемонстрировать ее могущество окружающим.

Гидростатика

Хотя, как мы видим, Архимед ввел понятие центра тяжести и нашел закон рычага, в физику под именем закона Архимеда и архимедовой силы вошли понятия из его замечательного сочинения «О плавающих телах». Как и сочинение «О равновесии плоских фигур», это сочинение состоит из двух частей: вступительной, в которой даются основные положения, и основной, посвященной рассмотрению равновесия плавающего в жидкости параболоида вращения.

Замечательно, что роль аксиомы здесь берет на себя физическая модель «идеальной жидкости». «Предположим, – пишет Архимед, – что жидкость имеет такую природу, что из ее частиц, расположенных на одинаковом уровне и прилежащих друг к другу, менее сдавленные выталкиваются более сдавленными и что каждая из частиц сдавливается жидкостью, находящейся над ней по отвесу, если только жидкость не заключена в каком-нибудь сосуде и не сдавливается чем-нибудь другим». Это единственное предположение, исходя из которого Архимед выводит все остальное.

Первым выводом является доказательство того, что «поверхность всякой жидкости, установившейся неподвижно, будет иметь форму шара, центр которого совпадает с центром Земли». Далее следуют теоремы: «Тела, равнотяжелые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости и не будут двигаться вниз», «Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погружений части тела, имел вес, равный весу всего тела», Тела, более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела», «Тела, более тяжелые, чем жидкость, опущенные в жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину а жидкости в объеме, равном объему погруженного тела».

Трудно представить себе более ясные и четкие формулировки поведения в воде плавающих тел. Но возникает вопрос: правомочно ли было выводить их из принятого вначале положения о свойствах жидкости. Как можно доказать его правильность?

И тут мы впервые в истории физики встречаемся со своеобразием ее аксиом.

Архимед предлагает нам мысленно представить себе вещество, состоящее из абсолютно скользких атомов, способных передавать давление во все стороны и подвергающихся давлению со стороны таких же атомов, находящихся сверху. Потом он математически исследует это вещество. Оказывается, что поверхность такого вещества в свободном состоянии есть сфера с центром в центре земного шара. Но так как это общеизвестный факт (форма поверхности Мирового океана), то отсюда можно сделать обратный вывод: поскольку поверхность океана – сфера, то жидкость имеет именно такое строение, какое постулировано Архимедом. Можно также не сомневаться в том, что выведенные математические законы гидростатики Архимед проверял на опыте.

Таким образом, сочинение «О плавающих телах» – первая попытка экспериментально проверить фундаментальное предположение о строении вещества путем создания его модели. В этом сочинении Архимед не только подтвердил атомистические идеи Демокрита, но и доказал ряд важных положений о физических свойствах атомов жидкости.

Архимед вывел законы гидростатики для идеальной жидкости, описав ее свойства. Свойства реальной жидкости немного отличаются от свойств архимедовой идеальной жидкости. Эти отличия в некоторых случаях играют заметную роль. Так, вопреки законам Архимеда смазанная жиром иголка может держаться на поверхности налитой в сосуд воды. Но нельзя упрекнуть ученого в неверности его законов. Эти законы справедливы постольку, поскольку жидкость приближается к идеальной модели. Для описания свойств реальной жидкости надо внести соответствующие поправки в модель. Но это не опровергает справедливость выкладок Архимеда.

Определение удельного веса

Римский архитектор Витрувий, сообщая о поразивших его открытиях разных ученых, приводит следующую историю: «Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.

Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания корона оказалась соответствующей выданному весу золота.

После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».

Затем, исходя из своего открытия, он, говорят, сделал два слитка, каждый такого же веса, какого была корона, один из золота, другой из серебра. Сделав это, он наполнил сосуд до самых краев и опустил в него серебряный слиток, и... соответственное ему количество воды вытекло. Вынув слиток, он долил в сосуд такое же количество воды.., отмеряя вливаемую воду секстарием (0,547л), чтобы, как прежде, сосуд был наполнен водой до самых краев. Так он нашел, какой вес серебра соответствует какому определенному объему воды.

Произведя такое исследование, он таким же образом опустил золотой слиток... и, добавив той же меркой вылившееся количество воды, нашел на основании меньшего количества секстантов воды (секстант – римская мера веса, равная 0,534 Н), насколько меньший объем занимает слиток».

Потом тем же методом был определен объем короны. Она вытеснила воды больше, чем золотой слиток, и кража была доказана.

Часто этот, рассказ связывают с открытием закона Архимеда, хотя он касается способа определения объема тел неправильной формы.

Возможно, что в этом рассказе Витрувия ванна, забытая одежда и возглас «Эврика!» являются вымыслом, но нас интересуют научные факты. Во-первых, бросается в глаза, что согласно описанию Витрувия Архимед сделал больше того, что требовалось. Чтобы обнаружить примесь, достаточно было сравнить объем короны с объемом равного ей веса золота. По-видимому, Витрувий не вполне разобрался в какой-то другой принадлежавшей Архимеду задаче об определении удельного веса тел. Об этом свидетельствует и фраза: «Отсюда он нашел, какой вес серебра соответствует какому объему воды». В ней, собственно, и содержится определение удельного веса – отношение веса к объему или к весу вытесненной воды (при измерении объема золотого слитка говорится о весе воды).

Оптика

В своем стремлении математически описать явления природы Архимед выделял задачи, наиболее поддающиеся геометрическому анализу. Поэтому занятия Архимеда в области геометрической оптики – «катоптрике», как ее называли прежде, можно считать закономерными.

Очень немного можно сказать о «катоптрике» Архимеда. От нее в позднем пересказе уцелела единственная теорема, в которой доказывается, что при отражении света от зеркала угол падения луча равен углу отражения. Свои оптические теории (как и механические) Архимед строил на основе аксиом. Одной из таких аксиом являлась обратимость хода луча – глаз и объект наблюдения можно поменять местами. Весь же круг вопросов «катоптрики» был очень широк. Перечисление проблем, которых касался Архимед в этой книге, мы находим у других авторов античного периода. Вот как об этих работах говорил Апулей: «Почему в плоских зеркалах предметы сохраняют свою натуральную величину, в выпуклых – уменьшаются, а в вогнутых – увеличиваются; почему левые части предметов видны справа и наоборот; когда изображение в зеркале исчезает и когда появляется; почему вогнутые зеркала, будучи поставлены против Солнца, зажигают поднесенный к ним трут; почему в небе видна радуга; почему иногда кажется, что на небе два одинаковых Солнца, и много другого подобного же рода, о чем рассказывается в объемистом томе Архимеда». Из других свидетельств следует, что Архимед изучал также и явление преломления лучей в воде.

С «катоптрикой» связана легенда о поджоге Архимедом римских кораблей во время осады Сиракуз. Что в ней вымысел и что, быть может, является отражением действительных событий, мы рассмотрим в отдельной главе.

Можно не сомневаться в том, что «катоптрика» Архимеда оказала большое влияние на последующее развитие оптики.

Влияние работ Архимеда на развитие физики

Если говорить об ученых, опередивших свое время, то Архимед, вероятно, может считаться своеобразным рекордсменом. Его идеи нашли продолжателей лишь через 1800 лет.

Предложенное Архимедом направление в науке – математическая физика, которую он провозгласил и в которой так много сделал, не была воспринята ни его ближайшими потомками, ни учеными средневековья.

Архимеда знали как гениального математика, им восхищались, его изучали и комментировали, но его физические работы долгое время не получали развития.

В какой-то мере в средние века на сочинениях Архимеда базировались работы ряда ученых Востока о взвешивании и определении удельного веса веществ. Математик и астроном IX в. Сабит ибн-Корра перевел на арабский язык и прокомментировал многие сочинения Архимеда и составил трактат о рычажных весах. На основе сочинения Архимеда «О плавающих телах» крупнейшие ученые того же времени ал-Бируни и Омар Хайям провели определения удельных весов большого количества металлов и драгоценных камней. При этом ал-Бируни пользовался методом сравнения значений веса равных объемов различных минералов, а Омар Хайям – методом взвешивания образцов на воздухе и в воде.

В эпоху Возрождения, когда центр научной мысли вновь переместился в Европу, европейская наука училась у арабской. Некоторые труды Архимеда дошли до нас только в арабских переводах. Одним из первых продолжателей механики Архимеда был итальянский ученый и инженер Гвидо Убальди дель Монте (1545...1607), исследовавший вопросы равновесия и решивший задачу о грузе на наклонной плоскости. Многое сделал для развития статики Архимеда другой итальянский ученый – Джовани Баттиста Бенедетти (1530...1590). Крупнейшим механиком «школы Архимеда» был фламандский ученый Симон Стевин (1548...1620). В своем классическом труде «Начала статики» он не только исходит из ряда аксиом Архимеда, но и развивает его работы, анализируя целый ряд механизмов. В число постулатов Стевин вводит принцип невозможности вечного двигателя; ему принадлежит также введение обозначений сил в виде стрелок. Много Стевин сделал и в области гидростатики, развив положения Архимеда, данные им в «Плавающих телах». Интерес Стевина к этим проблемам был далеко не абстрактным, так как он занимал должность инспектора плотин и консультанта голландского адмиралтейства.

Главным достижением классической механики была математическая разработка законов динамики Галилеем и Ньютоном. И хотя здесь достижения Архимеда непосредственно не использовались, его математический подход к проблемам торжествовал. Знаменательно, что Галилей хорошо знал труды Архимеда и часто к ним обращался. Например, при рассмотрении |равноускоренного движения он писал: «Я не предполагаю ничего иного, кроме определения движения; я хочу трактовать и рассматривать это явление в подражание Архимеду, который, заявив в «Спиральных линиях», что под движением по спирали он понимает движение, слагающееся из двух равномерных (одного – прямолинейного, а другого – кругового), непосредственно переходит к демонстрации выводов. Я заявляю о намерении исследовать признаки, присущие движению тела, начинающемуся с состоянии покоя и продолжающемуся с равномерно возрастающей скоростью, а именно так, что приращения этой скорости возрастают не скачками, а плавно, пропорционально времени».

Научный успех Архимеда почти полностью основан на используемой им методологии. В целом применяемые ученым методы можно разделить на две группы: первая направлена на поиск интересующего его решения (механический метод), а вторая - на доказательство верности полученного результата. В работах Архимеда часто встречаются цитаты из текстов Евклида и других более ранних математиков, то есть он приводит многие решения как само собой разумеющееся и для краткости говорит о них в своих трудах, словно они всем известны. Таким образом, мы видим математика, который работает с достойными доверия источниками и умеет извлекать из них материал, необходимый для его собственных исследований. В наши дни для любых доказательств мы используем алгебраический язык (формулы с буквами, цифрами и математическими символами), но в рассматриваемое нами время, когда жил Архимед, такого языка еще не существовало. Вот почему его тексты нелегки для современного читателя, ведь все его рассуждения основываются на чисто геометрических понятиях. Далее мы представим некоторые математические открытия Архимеда и постараемся реконструировать путь его мысли, хотя для этого нам и придется прибегать к языку алгебры.

Метод механических теорем

Из книги «Метод механических теорем» можно понять, что Архимед не скрывал свои методы от научного сообщества того времени, как мы уже показывали на примере константинопольского палимпсеста. В частности, он отправил этот труд Эратосфену, решив, что в данном случае он попадет в хорошие руки и сможет послужить получению новых интересных результатов.

Несмотря на то что Герои цитирует эту книгу в своем трактате «Метрика», многие источники описывают Архимеда ученым, ревниво относившимся к своей работе и не склонным популяризировать свою методологию. К счастью, в 1906 году исследователь-эллинист Гейберг обнаружил «Метод» и другие труды ученого, содержащиеся в палимпсесте. На самом деле Архимед охотно обнародовал и свои открытия, и научные методы, приведшие к этим открытиям. Он даже побуждал Эратосфена воспользоваться его методикой, уверяя последнего, что «можно было бы использовать этот путь для того, чтобы достичь определенных научных результатов посредством механики».

[...] написав это, обнародовать данный метод потому, что я о нем уже раньше упоминал - а я не хочу, чтобы казалось, будто я занимался пустой болтовней, - а также и потому, что я убежден: он принесет немалую пользу для математики.

Из письма Архимеда Эратосфену в «Методе»

Таким образом, в данной работе Архимед объясняет собственный механический метод. Кроме механического метода трактат содержит и геометрический (метод исчерпывания), приписываемый Евдоксу. Механический метод здесь использован исключительно для приблизительного решения задач, которые требуют затем более строгого и убедительного доказательства геометрическими методами:

«[...] Ведь некоторые вещи, которые я сначала представлял механическим способом, затем были мной доказаны с помощью геометрии, [...] легче построить решение, уже имея определенные знания об исследуемых вещах, чем искать его без какого-либо начального знания».

Здесь важно заметить, что он приводит как нечто само собой разумеющееся некоторые результаты из собственной работы «О равновесии плоских фигур». Трактат дошел до нас не полностью - из него сохранились 16 утверждений с некоторыми важными уточнениями. В первых 11 автор представляет механический метод сам по себе, а в остальных описывает весь процесс, включая последующее доказательство с помощью вышеупомянутого метода исчерпывания. Архимед затрагивает большое количество вопросов, которые он уже исследовал в предыдущих трудах: например, квадратура сегмента параболы - темы, изложенной в книге «О квадратуре параболы». Первое утверждение трактата, проиллюстрированное на рисунке на следующей странице, звучит так:

«Пусть АВС - сегмент, заключенный между отрезком прямой АС и параболой АВС; поделим АС напополам точкой D и проведем прямую DBE параллельно оси параболы, а также отрезки АВ, ВС. Я утверждаю, что сегмент параболы АВС по площади равен четырем третьим треугольника АВС». («Метод механических теорем», утверждение 1.)

СТОМАХИОН

С небольшим трактатом «Стомахион» произошло то же самое, что и с «Методом»: на протяжении истории было множество свидетельств его существования, но найден он был лишь в 1906 году с открытием константинопольского палимпсеста. В IV веке Авзоний и Марий Викторин говорили о Loculus Archimedius (шкатулке Архимеда) из 14 пластинок слоновой кости, которые вместе составляют квадрат. Все, что осталось от трактата,- это изложение способа деления квадрата на 14 частей (рисунок 1). Кроме того, там приводятся соотношения площадей фрагментов и полного квадрата. Не очень понятно, было ли это главным содержанием «Стомахиона»: хотя некоторые усматривают здесь начало комбинаторики, другие считают данное описание не более чем развлечением, чем-то вроде пазла или танграма.

РИС. 1

Если мы наложим фигуры из «Стомахиона» на квадрат стороной в 12 клеток, площадь каждой фигуры будет такой же, какой она обозначена на рисунке. Простой способ воспроизвести данные фигуры - взять листок бумаги в клеточку. Числа на фигурах обозначают их площадь.

Лишь в 2003 году удалось провести строгий комбинаторный анализ, который показал, что существуют 17152 способа сложить фигуры из «Стомахиона» в целый квадрат, и это если не принимать во внимание возможность их поворота или зеркального отражения (рисунок 2).

Перемещая фрагменты, можно не только составить квадрат, но и создавать веселые фигурки вроде этого слона.

Воспроизведение геометрического чертежа, которым воспользовался Архимед, чтобы выяснить соотношение площадей сегмента параболы и вписанного в него треугольника. Основой для данного решения служит механический метод.

Исчерпывающая математика: метод исчерпывания

В древнегреческой математике в какой-то момент начался серьезный кризис, связанный с так называемыми невыразимыми числами, которые не могут быть представлены отношением целого числа к натуральному. В настоящее время такие числа называются иррациональными. Такое их свойство вызвало большие проблемы при сравнении криволинейных и прямолинейных фигур. Это значит, что греки сталкивались с серьезными сложностями, если хотели вычислить площадь круга или иных фигур, ограниченных кривыми, а также и некоторые другие величины, например диагональ квадрата. Данная проблема была частично решена благодаря методу исчерпывания, который можно считать предшественником современного исчисления бесконечно малых величин и вычисления предела. Уже Евклид использовал его в некоторых построениях в своих «Началах», а Архимед применял его в течение всей своей математической карьеры. И именно он назвал автором этого метода Евдокса во вступлении к своему трактату «Метод механических теорем».

Невозможно найти во всей геометрии более сложные и более важные вопросы, изложенные столь простыми и столь понятными словами, как в теоремах, созданных божественным разумом Архимеда.

Архимед был человеком такого возвышенного образа мыслей, такой глубины души и богатства познаний, что о вещах, доставивших ему славу ума не смертного, а божественного, не пожелал ничего написать, но, считая сооружение машин и вообще всякое искусство, сопричастное к повседневным нуждам, низменным и грубым, все свое рвение обратил на такие занятия, в которых красота и совершенство пребывают не смешанными с потребностями жизни. И нельзя не верить рассказам, будто он был тайно околдован некоей сиреной, не покидавшей его ни на миг, а потому забывал о пище и об уходе за телом. Он совершил множество замечательных открытий, но просил друзей и родственников поставить на его могиле лишь цилиндр с шаром внутри и написать расчет соотношения их объемов.

Архимед не придавал большого значения всем сооруженным им машинам, он рассматривал их лишь как простые геометрические игрушки, которыми он занимался в свободное время, и то большей частью по настоянию царя Гиерона , постоянно направлявшего его занятия от чисто интеллектуальных предметов к материальным вещам.

В минуту опасности, грозящей родному городу, Архимед смог выйти из своего «кабинета» и отдать все силы его защите.

Все это настолько красиво, что невольно возникает вопрос: «А верно ли это? Не является ли это легендой, создавшейся вокруг Архимеда?». А что такие легенды действительно создавались, можно видеть тоже из весьма распространенного объяснения того, каким образом Архимед открыл носящий его имя закон: всякое тело, погруженное в жидкость, теряет в своем весе столько, сколько весит жидкость в объеме этого тела. Это объяснение основывается на следующем рассказе римского архитектора Витрувия .

«Когда Гиерон , достигший царской власти в Сиракузах, после удачного завершения своих походов, решил по обету бессмертным богам поместить в одном из храмов богатый венец, он заказал сделать его за определенную плату и отвесил нужное количество золота подрядчику. В назначенный по договору Архимед (3 в. до н. э.) срок тот доставил царю тонко исполненную работу, в точности, видимо, соответствовавшую весу отпущенного на нее золота.

После же того, как царь узнал о том, что часть золота была утаена и при изготовлении венца в него было примешано такое же количество серебра, он, негодуя на нанесенное ему оскорбление и не находя способа доказать эту покражу, обратился к Архимеду с просьбой взять на себя разрешение этого вопроса.

Случилось так, что в то время как Архимед думал над этим, он, садясь в ванну, заметил, что чем глубже он погружается в нее своим телом, тем больше через край вытекает воды. Эта идея послужила ему способом разрешения его вопроса, и он, не медля, вне себя от радости, выскочил из ванны и бросился к себе домой, громко крича, что нашел то, что искал, ибо на бегу он то и дело восклицал по-гречески «эврика, эврика».

Отметим, что в рассказе Витрувия не упоминается о законе Архимеда. В действительности, как можно видеть из «Метрики» Герона Александрийского (около 100 г. н. э.), Архимед считал, что если подлежащее измерению тело удобопереносимо, то нужно сделать прямоугольный сосуд, могущий вместить это тело, наполнить его водой и опустить в него неправильное тело; тогда ясно, что некоторое количество воды выльется так, что какой был объем у опущенного в воду тела, столько воды недостанет в этом вместилище после того, как тело будет из него вынуто.

Если измерить сделавшееся пустым пространство, то можно найти объем опущенного тела, а следовательно, и плотность.

Теперь постараемся представить себе Архимеда освобожденным от наросших легенд. Его ученик Гераклид составил утраченную/теперь биографию своего учителя.

Эта биография была, по-видимому, очень иконописна, так как автор приписал Архимеду даже открытие конических сечений, что никак не может соответствовать действительности. Попробуем восстановить биографию Архимеда, исходя из надежно установленных фактов.

Архимед погиб в 212 г. до н. э. - в год взятия Сиракуз римской армией. Византийский писатель XII в. Цеци сообщает, что он умер 75 лет от роду; на этом основании принято считать, что Архимед родился в Сицилии в 287 г. до н. э. Когда Архимеду было около десяти лет, в Сицилию вторгся знаменитый царь Пирр Эпирский.

В борьбе с Пирром выдвинулся Гиерон , бывший родственником Архимеда, и в 270 г. до н. э. сделавшийся правителем Сиракуз. Первая половина его царствования не была мирной; он втянулся в первую Пуническую войну (264-241 гг. до н. э.), где в союзе с карфагенянами воевал против римлян, но скоро вышел из войны. По окончании войны Сицилия сделалась римской провинцией, Сиракузы еще оставались свободными.

С 241 г. до н. э. начинается мирный период царствования Гиерона , старавшегося поддерживать хорошие отношения как с римлянами, так и с карфагенянами; тем не менее он деятельно готовится к отражению возможных покушений на свободу Сиракуз и усиливает обороноспособность родного города, привлекая к этой работе, как писал Плутарх, и Архимеда.

Таков был фон, на котором развертывалась деятельность Архимеда. Из дошедших до нас полностью сочинений Архимеда рассмотрим следующие .

1. «Квадратура параболы».

2. Две книги «О шаре и цилиндре».

3. «О коноидах и сфероидах».

4. «О спиралях».

Эти сочинения представляют законченную группу посланий, написанных Архимедом к некоему Досифею - ученику Конона Самосского, бывшего кем-то вроде научного руководителя Архимеда и давшего ему программу работ, воплощенную в этих посланиях. Порядок написания этих сочинений вполне устанавливается из сопровождающих их введений.

Первое из этих сочинений было написано к Досифею после смерти Конона . Конон Самосский был известен историкам по следующей легенде. В 246 г. до н. э. египетский властитель Птолемей III Эвергет начал Третью Сирийскую войну и отправился в поход на Антиохию ; его супруга Вереника , молясь, за благополучное окончание похода, принесла в жертву богам свои волосы. После окончания похода оказалось, что ее волос в храме нет; тогда придворный астроном Конон заявил, что эти волосы были помещены богами на небе и образовали новое созвездие «Волосы Вереники ». Это событие было воспето придворным поэтом Каллимахом , вследствие чего и стало известным историкам.

Конон был в действительности очень крупным ученым, оказавшим большое влияние на научное развитие Архимеда, который мог познакомиться с ним в Сицилии, где Конон производил астрономические исследования, или в Александрии во время пребывания там Архимеда.

Второй ученый, с которым Архимед поддерживал переписку, был знаменитый Эратосфен Киренский (285-205 гг. до н. э.), который был приглашен в Александрию в 245 г. Птолемеем Эвергетом для воспитания его сына и наследника Птолемея IV Филопатора . Наиболее удобное время для этого посещения наступило после окончания первой Пунической войны, когда правитель Сиракуз Гиерон мог отпустить Архимеда в Александрию.

Легенда о Веренике важна в том отношении, что в 246 г. до н. э. Конон был жив, следовательно, сочинение" «О квадратуре параболы» было написано после этого года. Но в 246 г. Архимеду шел уже 41 год; таким образом, научной работой Архимеду пришлось заняться уже на склоне лет, приближаясь к пятидесятилетнему возрасту. Обычно историки относят смерть Конона к тридцатым годам III в. до н. э.; тогда предположительно можно было бы отнести «Квадратуру параболы» примерно к 235 г. до н. э.

Определим примерное время остальных произведений Архимеда:

5. Две кциги «О равновесии плоских фигур».

6. «Эфод , или послание к Эратосфену о механических теоремах».

7. Две книги «О плавающих телах».

8. «Измерение круга».

9. «Псаммит».

10. «Задача о быках».

Две книги «О равновесии плоских фигур» имеют своей целью определить центр тяжести параболического сегмента; таким образом, они написаны после «Квадратуры параболы».

Во вступлении к «Эфоду » Архимед писал о найденных им теоремах. Эти теоремы оказались отличными от найденных ранее: действительно в прежних теоремах коноидальные и сфероидальные тела, а также их сегменты сравнивались по величине с конусами и цилиндрами, и ни одно из этих тел не оказалось равным телесной фигуре, ограниченной плоскостями; из рассматриваемых же тел, ограниченных двумя плоскостями и цилиндрическими поверхностями, каждое оказывается равным одной из телесных фигур, ограниченных плоскостями.

Таким образом, «Эфод » написан после «Коноидов и сфероидов».

Вторая книга «О плавающих телах» рассматривает положение равновесия сегмента параболоида, для чего необходимо знать положение центра тяжести соответствующего объема. Так как это положение определено в «Эфоде », то книги о плавании написаны после «Эфода ».

Таким образом, порядок этих сочинений можно считать установленным - все они написаны после «Квадратуры параболы».

Оставшиеся три произведения относится к вычислительной математике. Из них особенно интересна книга «Об измерении круги», написанная, как писал сам Архимед, ранее «Псаммита».

В первых четырех указанных сочинениях (в посланиях к Досифею ) Архимед занимается определением поверхностей и объемов различных фигур и тел. Его решение состоит из двух стадий: в первой он решает задачу сначала механическим способом, разбивая исследуемую фигуру на весьма малые части, очень похожие на «неделимые» Демокрита ; получив таким образом решение задачи, он доказывает его строго геометрически, пользуясь методом исчерпания Евдокса , строя последовательные совокупности прямолинейных фигур или пластинок так, чтобы они «исчерпали» всю площадь или объем измеряемой фигуры. В «Квадратуре параболы» он делает это, беря метод исчерпания в его первоначальной форме. Рассмотрим этот метод.

Пусть АОВ (рис. 3) представляет сегмент параболы, площадь которого нужно определить; пусть ОС ось параболы, которую принимаем за ось х , тогда соотношение между абсциссами х и ординатами у параболы будет иметь вид:

Рис.3

Архимед пользуется свойством параболы, что все ее диаметры параллельны. Он вписывает в параболу треугольник АОВ , вершина которого совпадает с вершиной параболы; площадь этого треугольника примем за единицу. Так как ось Ох - ось параболы, то С - середина прямой АВ , ОС - диаметр сегмента АОВ .

После выделения треугольника АОВ получим еще два сегмента параболы. Разделим хорды ОА и ОВ пополам в точках D и D" и проведем отрезки DE и D"E" . Соединив прямыми точки Е и E" соответственно с А , О и В , получим еще два треугольника АЕО и ВE"О . Проведем прямые DD" и ЕE" полученная фигура будет, очевидно, параллелограммом.

Но EG представляет ординату, соответствующую абсциссе OG , а АС - ординату для абсциссы ОС . Так как AC =2EG , то по уравнению (1) параболы

или

Переместим треугольники АЕО и BE"О параллельно оси Ох так, чтобы они стали основаниями на прямой АВ . Так как высоты ED и ЕD" равны , то нетрудно видеть, что сумма площадей этих треугольников в передвинутом положении равна четверти АОВ , или, поскольку площадь АОВ принята за единицу, .

Сумма площадей полученных трех треугольников равна:

Если рассмотреть еще четыре сегмента на хордах АЕ, ЕО, ОE" и Е"В и вписать в них треугольники, то аналогичное рассуждение покажет, что сумма площадей четырех этих треугольников равна суммы треугольников АЕО и ОЕ"В ; добавив эти треугольники, получим сумму

Продолжая рассуждать таким же образом, получим, что площадь рассматриваемого сегмента равна сумме геометрической прогрессии:

Таким образом, если на основании АВ сегмента и его оси ОС построить прямоугольник (параллелограмм), то площадь параболического сегмента будет равна 2/з площади этого параллелограмма.

В книгах «О шаре и цилиндре» наблюдается следующая эволюция метода исчерпания. Определяемая величина заключается между двумя суммами, из которых одна больше, а другая меньше определяемой величины, причем отношение этих сумм может быть сделано сколь угодно близким к единице.

Тот же метод использован в книгах «О спиралях» и «О коноидах и сфероидах», но только теперь определяющее условие заключается в том, что разность этих сумм может быть сделана сколь угодно близкой к нулю.

Так как в книге «Об измерении круга» употребляется третья форма метода исчерпания, то имеются все основания полагать, что эта книга была написана не ранее сочинений «О спиралях» и «О коноидах и сфероидах». Кроме того, интересна близость тем книги «О спиралях» и «Измерения круга»: и та и другая касаются определения длины окружности, но только в первой книге длина окружности получается при помощи построения, а во второй - при помощи вычисления.

Таким образом, самым ранним из сохранившихся полностью сочинений Архимеда является «Квадратура параболы», написанная им в возрасте 45 лет. Чем же занимался Архимед ранее? В рассказе Полибия об осаде Сиракуз говорится, что первая Пуническая война не разрешила вопроса о форме отношений между Римом и Карфагеном. Карфагеняне не могли примириться с потерей Сицилии, а немного позже и Сардинии с Корсикой, захваченных Римом.

В 218 г. до н. э. началась вторая Пуническая война походом. Ганнибала из Испании через Альпы на Италию. Ряд блестящих побед Ганнибала, из которых наиболее важной была победи, одержанная при Каннах (216 г. до н. э.), поставил Рим в очень тяжелое положение, но все же римляне не сдавались. Ганнибалу пришлось искать союзников. На следующий год после победы при Каннах умер девяностолетний Гиерон, сохранивший верность Риму, но после его смерти в Сиракузах одержала верх антиримская партия и Сиракузы примкнули к восстанию греческих колоний в Сицилии. Против Сиракуз отправили войско под командой Аппия Клавдия и флот под командованием Марка Марцелла. Римляне хотели взять Сиракузы первым же приступом, надеясь при многочисленности рабочих рук покончить с приготовлениями в течение пяти дней. Но при этом они не приняли в расчет искусства Архимеда, не догадались, что иногда дарование одного человека способно сделать больше, чем огромное множество рук. Архимед заготовил внутри города, а равно и против нападающих с моря, такие средства обороны, что защитникам не было необходимости утруждать себя непредусмотренными работами на случай неожиданных способов нападения; у них заранее готово было все к отражению врага в любом случае.

Дальше Полибий рассказывает о нападении римского флота с моря. Архимед соорудил машины, приспособив их к метанию снарядов на любое расстояние. Так, если неприятель подплывал издали, то Архимед поражал его из дальнобойных камнеметальниц тяжелыми снарядами или стрелами и повергал его в трудное положение. Когда же снаряды начинали летать поверх неприятеля, то Архимед применял меньшие машины, каждый раз сообразуясь с расстоянием, и наводил на римлян такой ужас, что они никак не решались идти на приступ или приблизиться к городу на судах. Наконец, Марк (Марцелл), раздосадованный неудачами, вынужден был сделать попытку тайком ночью подойти к городу на кораблях. Когда римляне подошли к берегу на расстояние выстрела, Архимед употребил другое средство, направленное против воинов, сражавшихся с судов, а именно: он велел сделать э стене приблизительно на высоте человеческого роста множество отверстий, с наружной стороны имевших в ширину пальца четыре; у отверстий изнутри стены поставил стрелков, через отверстия обстреливал корабельных воинов и тем отнимал у них всякую возможность сделать что-нибудь. Таким образом, далеко или близко находился неприятель, Архимед не только разрушал все его планы, но и производил в егорядах большие опустошения.

В настоящее время то, что сделал Архимед, называется пристрелкой по квадратам: вся местность, окружающая крепость, делится на квадраты и для каждого квадрата определяется возвышение (угол с горизонтом дула) для орудия, из которого должен производиться выстрел. Разница заключается лишь в том, что во времена Архимеда вместо изменения возвышения надо было пользоваться изменением калибра орудия. Во всяком случае, когда неприятель показывался в каком-либо квадрате, пускались в ход орудия калибра, соответствующего этому квадрату. Такого рода пристрелка предполагает долгую предварительную работу по определению расстояний для различных квадратов и по подбору наилучшего калибра орудий.

Когда корабль приближался к городской стене, то, кроме действия метательных орудий, с машины спускалась прикрепленная к цепи железная лапа; управляющий жерлом машины захватывал в каком-либо месте этой лапой нос корабля и потом опускал вниз находящийся внутри города конец машины. Когда нос судна был таким образом поднят и судно поставлено отвесно на корму, то плечо рычага закреплялось неподвижно, а лапа вместе с цепью отделялась от машины освобождающим приспособлением. Вследствие этого некоторые суда ложились на бок, другие совсем опрокидывались, большинство же от падения в море носом со значительной высоты погружались и наполнялись водой, внося большой беспорядок и ужас среди экипажа. Изобретательность Архимеда приводила Марка в отчаяние; с прискорбием он видел, что осажденные глумятся над его усилиями и причиняют ему большие потери.

Римляне сильно страдали от камнеметальниц и катапульт, из которых их обстреливали; сиракузяне имели в запасе множество превосходных и метких метательных орудий, на которые царь Гиерон дал средства, а Архимед изобрел и мастерски построил машины.

Расчет машин, подымающих корабли, немыслим без учета потери веса корабля, погруженного в море; это можно сопоставить с открытием закона Архимеда.

Рассмотрим теперь подробно две книги Архимеда «О равновесии плоских фигур» (или о центре тяжести плоских фигур). Считают, что первая книга этого произведения посвящена теории рычага; некоторые авторы полагают даже, что эта книга, взятая в отдельности, является первым произведением Архимеда, а вторая книга, содержащая определение центра тяжести параболического сегмента, представляет самостоятельное произведение.

Однако в первой книге определяются только центры тяжести тех плоских фигур (параллелограмм, треугольник), которые нужны для доказательства теорем второй книги. Кроме того, многие положения во второй книге являются обобщением, сделанным на основании мыслей, изложенных в первой книге (первое предложение второй книги является обобщением пятого и шестого предложений первой книги). Первую книгу нельзя считать первым сочинением на рассматриваемую тему, так как в ней не дано самого главного - определения центра тяжести. Это было сделано в произведении, предшествовавшем созданию «Квадратуры параболы», в котором имеются ссылки на это произведение. Отрывки из него сохранились в «Механике» Герона Александрийского и «Математической библиотеке» Паппа. Наиболее важным из этих отрывков является сформулированное Архимедом определение понятия о центре тяжести: центром тяжести тела называется расположенная внутри него точка, обладающая тем свойством, что если за нее мысленно подвесить тяжелое тело, то оно остается в покое и сохраняет первоначальное положение.

Законы равновесия выводятся Архимедом из следующие допущений, помещенных в начале первой книги «О равновесии».

1. Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине.

2. Если при равновесии тяжестей на каких-либо длинах к одной из тяжестей что-либо прибавить, то они не будут уравновешиваться, но перевесит та тяжесть, к которой прибавлено.

3. Если от одной из тяжестей отнять что-либо, то они не будут уравновешиваться, но перевесит та тяжесть, от которой не было отнято.

4. При совмещении друг с другом равных и подобных плоских фигур совмещаются друг с другом и их центры тяжести.

5. У неравных, но подобных фигур центры тяжести располагаются подобно.

6. Если величины уравновешиваются на каких-либо длинах, то на тех же длинах уравновешиваются и величины, равные им.

7. Во всякой фигуре, периметр которой везде выпукл в одну и ту же сторону, центр тяжести находится внутри фигуры.

Приведем доказательство Архимеда в той форме, которую придал ему Галилей.

Пусть в точке О подвешено за середину коромысло MN имеющее длину 2(а+b) (рис. 4).

Рис. 4

К этому коромыслу при помощи бесконечного множества вертикальных веревочек прикреплена однородная балка KL такой же длины 2(а+b) . Вся система будет, очевидно, в равновесии, которое не нарушится, если разрежем балку по линии СС на два отрезка: КС - длины 2а и CL - длины 2b . После этого обрежем все веревки, кроме двух: АА и ВВ , находящихся в серединах отрезков КС и CL, отчего равновесие тоже не нарушится. Таким образом, величина КС = 2а на плече АО = b будет уравновешивать величину CL на плече ОВ - а . Иными словами, при равновесии грузы, приложенные в A и В , будут обратно пропорциональны соответствующим плечам.

Равновесие не нарушится, если обе отрезанные части повернем вокруг осей АА и ВВ на любые углы; именно это и предполагает допущение 6, равносильное такой формулировке. Действие груза, приложенного в данной точке, определяется только его величиной, т. е. совершенно не зависит от формы или ориентации этого груза.

Возможность поворачивания обеих осей балки вокруг осей АА и ВВ имеет место лишь при требуемом Махом законе пропорциональности моментов длине плеча в первой степени и исключает другие законы, например квадратичную зависимость; поэтому доказательство Архимеда является вполне строгим.

Закон равновесия рычага используется Архимедом в качестве основы метода геометрического интегрирования, изложенного им в «Эфоде», как средство для исследования и предварительного решения задач. Покажем его на простом примере, а именно на рассмотренной выше квадратуре параболического сегмента, но только сделаем упрощение: будем находить не площадь сегмента, равную двум третям параллелограмма, а площадь, которая остается у параллелограмма, если вырезать из него этот сегмент. Тогда задачу можно сформулировать в таком виде: найти площадь, заключенную между осью абсцисс, дугой параболы, заданной уравнением , и ординатой, соответствующей абсциссе ОA =l (рис. 5).

Рис. 5

Возьмем равноплечий рычаг AOG длиной 2l с точкой опоры О ; на одном из его плеч расположим площадь ОАВ и разобьем ее на ряд весьма тонких полосок шириной Δx . Пусть KL - одна из этих полосок, соответствующая абсциссе ОК = х ; тогда ордината KL = у выразится ах 2 и вся площадь полоски

Сдвинем ее на конец рычага А; момент этой полоски относительно точки О равен

Попробуем уравновесить этот момент, подвешивая с левой стороны рычага на том же расстоянии х полоску MN такой же ширины Δх . Длина соответствующей ординаты MN определится сравнением моментов обеих полосок относительно О :

откуда

Поступая так с каждой полоской, на левом плече рычага получим ряд полосок, непрерывно распределенных по длине GO . Так как ординаты этих полосок пропорциональны расстояниям х , то концы их расположатся по прямой линии ONT ; величина крайней ординаты GT = аl 2 .

Площадь S = ОАВ , сосредоточенная на конце A , уравновешена прикрепленным к стороне OG треугольником OGT . Площадь этого треугольника равна

a расстояние его центра тяжести от вершины О :

Сравнивая момент этого треугольника относительно О с моментом относительно той же точки, сосредоточенной в точке А искомой площади S , получим

откуда

или

что совпадает с найденным выше результатом.

Успех вывода получается в результате понижения степени рассматриваемой кривой - определение величины площади, ограниченной двумя прямоугольными отрезками и кривой второй степени, сводится к определению центра тяжести площади, ограниченной кривой первой степени, т. е. прямой. Этот метод приложим, очевидно, к кривым, уравнение которых имеет вид у = ax h .

Кроме перечисленных произведений, дошедших до нас полностью, сохранились отрывки более ранних произведений Архимеда, имеющиеся в «Механике» Герона и в 8-й книге «Библиотеки» Паппа.

У Герона есть отрывок из сочинения Архимеда «Книга опор», где не замечается никаких следов понятия о центре тяжести. Он пишет: если балка оперта по концам, то на каждую опору падает половина веса; если имеется еще третья опора между концами, то на нее падают по половине веса балки в обоих соседних пролетах; таким образом, средняя опора несет половину веса всей балки независимо от того, в каком месте она помещена.

Из книги Архимеда, название которой установить трудно (то ли это «О рычагах», то ли «О равновесии» или «Механика»), имеются большие отрывки: один в «Механике» Герона (книга I, стр. 24), а другой в «Математической библиотеке» Паппа (книга VIII, стр. 5-8). Эти отрывки показывают, как доказывались существование и единственность центра тяжести твердого тела произвольной формы.

Архимед рассматривает вертикальную плоскость ABCD , ограниченную сверху горизонтальной прямой АВ . Если на эту прямую положить тяжелое тело, то оно может оказаться в таком положении, что будет оставаться в покое, не вращаясь и не падая вниз. Если теперь мы мысленно продолжим плоскость ABCD , то она рассечет лежащее тело на две части, обладающие одинаковыми моментами и взаимно уравновешивающиеся. Если затем переставить груз так, чтобы он касался прямой АВ другой своей частью, то можно дать ему такое положение, что он, будучи опущен, останется в покое и не упадет. Если снова вообразить плоскость ABCD продолженной, то она тоже разделит груз на две взаимно уравновешивающиеся части и пересечется первой плоскостью, делившей тот же груз на две взаимно уравновешивающиеся части; если бы эти плоскости не пересекались, то те же самые части были бы и уравновешивающимися, и неуравновешивающимися, что нелепо.

Вообразим прямую АВ , перпендикулярную к горизонтальной плоскости; положим груз на точку А так, чтобы он, пользуясь прямой АВ как подставкой, оставался в покое. Если продолжить прямую АВ , то некоторая ее часть будет находиться внутри рассматриваемого тела. Снова наложим его на эту прямую другой частью так, чтобы оно опять стало неподвижным; тогда продолженная прямая АВ пересечется первоначально заключавшимся внутри тела отрезком.

Действительно, если бы она не пересеклась, то оказалось бы возможным, что некоторые плоскости, проведенные через каждую из этих прямых, не пересекаются друг с другом внутри тела, причем каждая из них разделяет груз на части, которые одновременно являются и уравновешивающимися, и неуравновешивающимися, что бессмысленно; следовательно, упомянутые прямые пересекутся внутри тела.

Если в других положениях помещать груз на точку А так, чтобы он оставался в покое, то снова продолженная прямая АВ обязательно пересечется заключающимися внутри тела отрезками первоначальных прямых. Из этого ясно, что такие воображаемые прямые пересекают друг друга в одной и той же точке; эта точка и называется центром тяжести .

Как следствие отсюда получается, что закрепленное в этой точке тело остается в равновесии в любом положении.

Вышеописанная методика применяется и в приведенных Героном («Механика», книга II, стр. 35-36) правилах нахождения центра тяжести различных плоских фигур. Для этого определяем центр тяжести, треугольника, равномерного по толщине и однородного по весу. Пусть дан треугольник ABC (рис. 6). Разделим линию ВС пополам в точке D и соединим А и D . Если опереть треугольник на линию AD , он не будет иметь момента ни в ту, ни в другую сторону, так как треугольники ABD и ADC равны. Точно так же если разделить линию АС в точке Е и соединить точки В и E , то, если опереть треугольник на линию ВЕ , он также не наклонится ни в ту, ни в другую сторону. Так как треугольник, будучи оперт на каждую из линий AD и BE , находится в равновесии своих частей и не наклоняется ни в ту, ни в другую сторону, то общая точка F , в которой эти две линии пересекаются, является центром тяжести.

Рис.6

Так как треугольники ABD и ADC равны, это заставило некоторых исследователей думать, что Архимед или кто-либо из его предшественников считал, что центр тяжести плоской фигуры будет точка, в которой пересекаются прямые, делящие площадь фигуры на две равные части. Невозможность такого предположения сразу же устанавливается, если прочесть, как определяется центр тяжести четырехугольника.

Пусть дан четырехугольник ABCD (рис. 7). Соединим точки В и D и разделим BD пополам в точке Е ; соединим также А и Е , Е и С и разделим линии АЕ и ЕС в точках F и Н таким образом, чтобы АЕ была равна удвоенной величине FE , а СН -удвоенной НЕ . Тогда центр тяжести треугольника ABD - точка F , а центр треугольника BDC - точка Н .

Рис. 7Рис.8

Получим то же самое, если представлять треугольник ABD сосредоточенным в точке F а треугольник BCD - в точке H . Тогда линия FH становится коромыслом, на концах которого находятся эти величины. Поэтому если разделить линию FH в точке G таким образом, чтобы GH относилось к FG как вес F , т. е. вес треугольника ABD к весу Н - к весу треугольника BDC , то точка G , в которой оба веса уравновешиваются, является центром тяжести этого четырехугольника.

Момент веса F равняется сумме моментов весов всех частей треугольника ABD , иными словами, в распоряжении Архимеда был весь материал современной теории параллельных сил. Поэтому при передаче результатов, полученных Архимедом, можно пользоваться современным изложением при непременном условии сохранения его чертежа.

Покажем, как Архимед определял центр тяжести сегмента параболы (предложение VIII второй книги «О равновесии плоских фигур»).

Пусть дан параболический сегмент АОВ с вершиной О (рис. 8). Проведем диаметр ОС и впишем в параболу треугольник AОВ . Выше показано, что площадь сегмента параболы равна 4/з треугольника АОВ . Предположим, что эта площадь равна трем, тогда площадь остающихся сегментов параболы AOF и ВОН будет равна единице. Разделим хорды ОА и ОВ пополам; проведем диаметры FD и НЕ , а также прямые DE и FH . Здесь

Пусть ОС = h ; центр тяжести параболического сегмента лежит на ОС , а сегментов AFO и ОВН - соответственно на диаметрах FD и ЕН .

Предположим, что расстояние от центра сегмента АОВ до основания АВ равняется kh , где k - неопределенный коэффициент; равным образом расстояния от прямой DE центров тяжести сегментов AOF и ВОН равны: -. Далее высота центра тяжести треугольника АОВ над основанием АВ равна 1/3 h , а расстояние СК = h/2 . Получим теперь, что момент площади сегмента АОВ относительно АВ равен сумме моментов площадей треугольника АОВ и обоих сегментов AFO и ВНО . В таком случае

Сокращая это выражение на А, после очевидных упрощений получаем

откуда

Таким образом, центр тяжести параболического сегмента находится на диаметре на расстоянии 2/5 его длины от основания. Второй работой Архимеда, имеющей определенное отношение к механике, является книга «О спиралях». В самом ее начале интересна терминология, показывающая развитие понятия о скорости. Как существительное «скорость» во времена Архимеда еще не употреблялось: было прилагательное, которое употреблялось как «более или менее скорый» и «равноскорый»; так назывались движения, при которых в одно и то же время проходились одинаковые пути, независимо от того, как эти движения происходили. Для обозначения равномерности движения Архимед употреблял выражение «равно- скоро само с собой», т. е. равноскорыми должны быть движения во всех промежутках времени, на которые можно подразделить все движение.

Основная тема этого произведения заключается в задаче: построить прямую, длина которой равнялась бы длине окружности. Для решения Архимед пользуется кинематическим методом; он строит кривую, так называемую архимедову спираль, радиус-вектор которой изменяется пропорционально полярному углу (рис. 9).

Рис.9

Пусть точка О представляет полюс спирали, радиус-вектор которой за время первого оборота сделался равным r = ОА , а прямая AD является касательной к спирали в точке А . Спираль образуется в результате сложения двух движений: равномерного - прямолинейного по прямой ОАС и равномерного - кругового. Если бы точка, описывающая прямую, остановилась, придя в точку А , то в переносном вращении она описала бы изображенную на чертеже окружность AKL с радиусом r .

Пусть АС и АЕ представляют весьма малые перемещения точки, описывающей спираль, в обоих составляющих движениях - по радиусу и перпендикулярно к нему по окружности. При сложении этих движений описывающая спираль точка из положения А перейдет в точку D и прямая AD будет касательной к спирали. Перпендикулярно к радиусу ОА проведем прямую ОВ и продолжим касательную AD до пересечения ее этой прямой в точке В . В начале первого оборота прямая занимала положение ОАС ; от ОА отсчитывались углы поворота вращающейся прямой.

По истечении времени первого оборота прямая придет в первоначальное положение, угол поворота станет равным 360° и точка А вращающейся прямой опишет окружность радиусом r . Таким образом, путь, пройденный точкой А в относительном движении по радиусу за время первого оборота, равен ОА, а в переносном движении по окружности - ее длине. Но эти пути относятся как скорости, или как перемещения за один и тот же промежуток времени, т. е. как АС и АЕ . Из подобия треугольников AED и BOA получаем:

Иными словами, если ОА - путь, пройденный точкой в прямолинейном относительном движении, то ВО - путь, пройденный за то же время точкой А в переносном движении, т. е. длина окружности AKLA .

Треугольник AED , по существу, представляет дифференциальный треугольник Барроу - Ньютона, и не исключена возможность, что понятие об этом треугольнике появилось у Исаака Барроу в результате чтения сочинений Архимеда, которые с переделанными доказательствами были им изданы в 1675 г. Во всяком случае изучение сочинений Архимеда математиками XVII в. было необходимой подготовительной работой к появлению классического анализа бесконечно малых.

Последним произведением Архимеда является его сочинение «О плавающих телах». В первой книге он устанавливает основные законы равновесия тел в жидкости и рассматривает условия равновесия сферического сегмента, погруженного в воду, поверхность которой он считает тоже сферической, как поверхность реальных земных морей. Во второй книге он формулирует носящий его имя закон и затем рассматривает условия равновесия плавающего в жидкости сегмента параболоида вращения, причем поверхность жидкости теперь уже считается плоской.

В основе его рассуждений лежат теоремы, определяющие величину объема и положение центра тяжести сегмента параболоида вращения.

При погружении тяжелого твердого тела в жидкость, плотность которой больше плотности тела, оно опускается в жидкость так, чтобы поверхность жидкости (так называемая плоскость плавания) отсекала от тела объем, вес жидкости в котором равнялся весу тела.

Если построить все плоскости плавания для различных положений плавающего тела, то огибающая всех таких плоскостей будет некоторой поверхностью, которая называется поверхностью сечений.

Центры тяжести объемов, отсекаемых плоскостями плавания, образуют поверхность, называемую поверхностью центров.

Для этих поверхностей имеются такие теоремы.

1. Плоскость плавания касается поверхности сечений в центре тяжести фигуры, отсекаемой поверхностью тела на плоскости плавания.

2. Касательная плоскость к поверхности центров параллельна соответствующей плоскости плавания.

Для нахождения всех плоскостей плавания в положениях равновесия плавающего тела нужно из центра его тяжести опустить нормали к поверхности центров и провести соответствующее этим нормалям плоскости сечения. Эти плоскости и будут искомыми плоскостями плавания.

Архимед рассматривал только те положения равновесия, когда основание сегмента находится или полностью вне поверхности жидкости (вершина сегмента обращена вниз), или полностью внутри жидкости (сегмент плавает с вершиной над поверхностью жидкости).

Так как сегмент принадлежит параболоиду вращения, то эту задачу можно свести к плоской, заменив все поверхности линиями, представляющими их сечения плоскостью, проведенной через ось параболоида. Обозначим сечение данного сегмента ABA , его ось ОВ , основание АОА и центр тяжести С 0 (ОС 0 = l/3ОВ ) (рис. 10). Пусть NN - сечение сегмента поверхностью жидкости, DB - ось погруженной части, a E (DE = l/3DB ) -центр тяжести объема погруженной части.

Рис. 10

Поверхность сечений изобразится параболой LDL , вершина которой D находится на поверхности жидкости; эта парабола представляет параболу ABA , сдвинутую вверх на расстояние BD . Чтобы получить поверхность центров, нужно через точку Е провести такую же параболу КЕК . Если Архимед рассматривает случай, когда основание АОА находится над поверхностью жидкости, то ему нужны часть D"DD" параболы сечений, ограниченная точками D" , D" , касательные в которых проходят через конец А основания, а также соответствующая часть Е"ЕЕ" параболы центров (D"E" параллельна ОВ ). Продолжить далее эти поверхности для него нельзя, так для этого пришлось бы определить объем сегмента, отсеченный плоскостью, которая пересекает как боковую поверхность сегмента, так и плоскость основания, а эта задача им не решалась.

Если требуется определить положение равновесия сегмента, плавающего вершиной вверх, то надо определять объем и центр тяжести погруженной части сегмента, которая будет иметь вид ANNA , иными словами, представит разность двух параболических сегментов BNN и ВАА . Основываясь на этом, можно построить новые кривые сечений и центров, которые тоже будут некоторыми параболами.

Далее следует рассматривать моменты пары, образованной весом сегмента и силой давления вытесненной воды, приложенной в центре тяжести погруженной части; равновесие имеет место, когда при отклонении от положения равновесия этот момент оказывается восстанавливающим. Таким образом, Архимед получает только положения устойчивого равновесия.

Разница между методом Архимеда и современным методом заключается в том, что сейчас плотность жидкости принимают постоянной и изменяют размеры рассматриваемого сегмента, а Архимед сохраняет постоянным положение тела, но изменяет плотность жидкости. Его методика, по существу, мало отличается от методики, выработанной в XIX в. при помощи теорем Дюпена.

Из этого не следует делать вывода о тождественности этих методов, как это делают некоторые исследователи, находящие у Архимеда даже понятие о метацентре, установленное лишь в XVIII в.

Основное различие заключается в том, что Архимед не мог построить поверхности сечений для всех положений тела относительно поверхности жидкости, а следовательно, и не знал ее, так как у греков построяемость была критерием существования того или другого геометрического образа или операции. Силой своего гения Архимед смог подняться до высот, достигнутых наукой в XIX в.

Для полной характеристики Архимеда следует отметить, что Архимед нашел значение . Что же заставило его найти числовое выражение отношения окружности к диаметру, тем более что он уже имел построение, позволяющее найти прямую, равную длине заданной окружности?

В истории европейской науки около 1600 г. математики тоже стремились найти более точное значение числа π. Это было время, когда Адриан Меций нашел значение , а Лудольф из Кельна вычислил число π с точностью до 36-го десятичного знака. Виллиброд Снеллий открыл метод триангуляции и применил его к определению размеров Земли.

Не было ли чего-нибудь подобного и во времена Архимеда? Тит Ливии, описывая осаду Сиракуз в 24-й книге своей истории Рима, называет Архимеда «единственным в своем роде созерцателем неба и светил». О найденной числовой величине я Архимед вспоминает в «Псаммите», где идет речь об определении размеров мира и вычислении количества песчинок, которые могли бы заполнить объем мира. Он проводит также наблюдения, чтобы вычислить величину Солнца и расстояние от него до Земли. Свои наблюдения он применяет к центру Земли; между прочим это первое появление в истории астрономии понятия о так называемом параллаксе; ближайший предшественник Архимеда Аристарх Самосский, проводя эти же наблюдения на поверхности Земли, считал, что они дают такие же результаты, как если бы наблюдения производились из центра Земли.

Для определения потребного количества песка Архимед создал систему счисления, при помощи которой можно было изображать очень большие числа. Этим занимался не один он: систему счисления больших чисел создавал его младший современник Аполлоний Пергский. Правда, инженерный ум Архимеда не ограничился простым вычислением; он, не придававший большого значения построенным им машинам, описал только одну из них - построенную им «астрономическую сферу». Эта сфера после взятия Сиракуз римлянами досталась в качестве добычи Марку Марцеллу, поместившему ее в Храме Доблести и сохранившему для себя лишь второй, меньший экземпляр.

В диалоге Цицерона «О государстве» одно из действующих лиц Сульпиций Галл (тоже занимавшийся астрономией и предсказавший даже лунное затмение) показывает эту сферу. Слушавший его рассказчик говорил об Архимеде, что в этом сицилийце был гений, равняться с которым человеческая природа не казалась способной. Для возможности представлений движений Солнца, Луны и пяти звезд ему пришлось отказаться от употребления сплошной сферы, на которой было бы невозможно их воспроизвести, и придумать другую совершенно отличного вида.

В изобретении Архимеда чудесным было искусство, в котором он мог объединить в одной системе и воспроизвести при помощи одного вращения все очень отличающиеся друг от друга движения и различные периоды обращения различных светил. Когда Галл приводил сферу в движение, то при каждом обороте можно было видеть, как Луна появлялась вслед за Солнцем на земном горизонте; как она появляется каждый день на небе; далее можно было видеть, как Солнце исчезало на небе и затем понемногу Луна погружалась в земную тень в тот самый момент, когда Солнце находилось с противоположной стороны.

С большими числами связано еще одно сочинение Архимеда, найденное в XVIII в. и опубликованное в 1773 г. известным немецким писателем Лессингом. Это так называемая «Задача о быках», посланная Архимедом на разрешение александрийским ученым, занимающимся подобными вопросами:

Сколько у Солнца быков, найди для меня, чужестранец?

(Ты их, подумав, считай, мудрости если не чужд).

Как на полях Тринакрийской Сицилии острова тучных

Их в четырех стадах много когда-то паслось.

Цветом стада различались: блистало одно млечнобелым,

Темной морской волны стада другого был цвет.

Рыжим третие было, последнее пестрым. И в каждом

Стаде была самцов множества тяжкая мощь.

Если Х , Y , Z и Т обозначим числа белых, черных, рыжих и пестрых быков, то они должны удовлетворять следующим уравнениям:

Так же раздельно коров, сколько каждого цвета их было,

Не назовет хоть никто в числах невеждой тебя,

Все ж к мудрецам причислен не будешь.

Эти неопределенные уравнения решить можно; наименьшие значения неизвестных, удовлетворяющих их, выражаются семи- и восьмизначными числами. Этого Архимед не считает достаточным для того, чтобы заслужить название мудреца. Поэтому он добавляет еще два условия:

1. Сумма быков белого и черного цвета должна быть точным квадратом:

2. Сумма пестрых и рыжих быков должна быть равна некоторому треугольному числу:

где п и п" - некоторые целые числа.

После этого Архимед продолжает:

Если ты это найдешь, чужестранец, умом пораскинув,

И сможешь точно назвать каждого стада число,

То уходи, возгордившись победой, и будет считаться,

Что в этой мудрости все ты до конца превзошел.

Решением этих задач занимались ряд математиков. В немецком переводе издания Архимеда Th. Heath указывается порядок общего числа быков:

Архимед поставил задачу, которая, как он знал, практически не может быть разрешена.