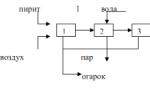
Формула для расчета взаимной корреляционной функции. Представление сигнала с помощью ортогональных функций. Взаимные корреляционные функции сигналов

В системах передачи информации очень часто возникает необходимость в сигналах со специально выбранными свойствами. При этом выбор сигналов диктуется не технической простотой их генерирования и преобразования, а возможностью оптимального решения поставленной задачи. К таким задачам обычно относят синхронизацию, распознавание, измерения, повышение скрытности и помехозащищённости и т.п.

Точность решения этих задач определяется степенью отличия друг от друга сигнала s(t) и его «копии» s(t-x), смещенной во времени .

Для количественной оценки степени различия сигналов s(t) и s(t- т) применяют автокорреляционную функцию (АКФ) В(т) сигнала s(t). Ее определяют как скалярное произведение сигнала и его задержанной копии:

Если s(t) носит импульсный характер, то этот интеграл заведомо существует.

Основные свойства автокорреляционной функции:

1. - при т =0 АКФ равна энергии сигнала.

2. - т.е. АКФ является чётной функцией.

3. - при любом т модуль АКФ не превосходит энергии сигнала.

В качестве примера рассмотрим вид АКФ прямоугольного видеоимпульса с амплитудой U и длительностью т н (рис. 1.13).

Рис. 1.13. АКФ прямоугольного импульса На рис. 1.13 затененные области показывают наложение сигналов, при котором произведение s(t)s(t-i) отлично от нуля. Это будет при |т|

Таким образом, АКФ является симметричной кривой с центральным максимумом, который всегда положителен. В зависимости от вида сигнала s(t) АКФ убывает монотонно или колебательно.

АКФ сигнала тесно связана с распределением его энергии по спектру частот соотношением

Можно оценивать корреляционные свойства сигналов, исходя из распределения энергии по спектру. Чем шире полоса частот сигнала, тем уже по времени АКФ. Сигнал с узкой АКФ лучше с точки зрения возможности точного измерения момента совпадения двух одинаковых по форме сигналов x(t-ij) и x(t-x) при изменении задержки ij. При проектировании современных систем радиосвязи сигнал выбирают широкополосным.

В принципе можно решать задачу синтеза сигнала с заданными корреляционными свойствами. Примером сигналов с наилучшей структурой АКФ могут служить дискретные сигналы (коды) Баркера, комплементарные коды и другие сложные сигналы. Корреляционные свойства этих сигналов оптимальны применительно к решению задачи обнаружения сигнала и измерения его параметров в радиолокации, в радиосвязи и других областях.

Два сигнала x(t) и y(t) могут отличаться как по своей форме, так и взаимным расположением на оси времени. Для оценки этих различий применяют взаимно корреляционную функцию (ВКФ) В ху (х). ВКФ двух вещественных сигналов x(t) и y(t) определяется как скалярное произведение вида

Свойства взаимно корреляционной функции сигналов с ограниченной энергией:

1. В ху (0) не обязательно является максимальным значением

2. - энергии сигналов хиу.

3. При перемене порядка индексации в обозначении ВКФ и соблюдении формы записи, указанной в выражении (31), происходит инверсия графика ВКФ относительно оси ординат х = О

4. (как и для АКФ)

АКФ является частным случаем ВКФ.

Корреляционная функция сигнала с неограниченной энергией.

Для таких сигналов определение АКФ по формуле (1.31) невозможно в силу бесконечности их энергии. К таким сигналам можно отнести периодические сигналы. Энергетическую оценку моделей таких сигналов проводят вводя среднюю удельную мощность

где Т - произвольный временной интервал.

Для периодических сигналов, энергия которых бесконечно велика по определению, усреднение удобно проводить по периоду Т

Для гармонического сигнала x(t) = Ucoscoot средняя удельная мощность Р = U 2 /2. Применяя формулу (33) к периодическому сигналу x ncp (t), представленному в видеряда Фурье

и принимая во внимание условие ортогональности

и

для средней мощности Р такого сигнала получим

Полная средняя мощность периодического сигнала равна сумме средних мощностей составляющих сигнал гармоник, включая, естественно, мощность постоянной составляющей (нулевой гармоники).

Для непрерывного и периодического сигнала АКФ определяется по формуле

с усреднением по бесконечному интервалу Т.

Для гармонического сигнала АКФ имеет вид

В отличие от АКФ и ВКФ финитных сигналов, АКФ периодической функции сама является периодической функцией и имеет размерность мощности. Значения аргумента т, для которых В(т) = 0, Определяют временные сдвиги сигнала и его копии, при которых корреляция отсутствует. Значение В(0) периодического сигнала численно равно мощности сигнала; для гармонического сигнала В(0) = U 2 /2.

В этой главе понятия, введенные в гл. 5 и 6 (вып. 1), распространяются на случай пары временных рядов и случайных процессов. Первым таким обобщением, приведенным в разд. 8.1, является взаимная корреляционная функция двумерного стационарного случайного процесса. Эта функция характеризует корреляцию двух процессов при различных запаздываниях. Второе обобщение представляет собой двумерный линейный процесс, образуемый с помощью линейных операций над двумя источниками белого шума. Важными частными случаями такого процесса являются двумерный процесс авторегрессии и двумерный процесс скользящего среднего.

В разд. 8.2 мы обсудим вопрос об оценивании взаимной корреляционной функции. Мы покажем, что если не применять к обоим рядам фильтрации, переводящей их в белый шум, то при оценивании могут возникать ложные завышенные значения взаимной корреляции. В разд. 8.3 вводится третье обобщение - взаимный спектр стационарного двумерного процесса. Взаимный спектр содержит два различных вида информации, характеризующей зависимость между двумя процессами. Информация первого типа содержится в спектре когерентности, являющемся эффективной мерой корреляции двух процессов на каждой из частот. Информация второго типа дается фазовым спектром, характеризующим разность фаз двух процессов на каждой из частот. В разд. 8.4 оба эти типа информации иллюстрируются на простых примерах.

8.1. ФУНКЦИЯ ВЗАИМНОЙ КОРРЕЛЯЦИИ

8.1.1. Введение

В этой главе мы будем заниматься вопросами описания пары временных рядов, или двумерного временного ряда. Используемые при этом способы являются обобщением способов, применявшихся в гл. 5, 6, и поэтому все относящиеся к временным рядам общие положения, изложенные в разд. 5.1, применимы и в этом случае. В разд. 5.1 под заголовком «Многомерные временные

ряды» кратко упоминалось о том, что отдельные временные ряды, образующие многомерный ряд, могут быть неравноправны по отношению друг к другу. Рассмотрим, например, систему, показанную на рис. 8.1, которая имеет два входа и два выхода

Рис. 8.1. Физическая система с двумя входами и двумя выходами.

Можно различать две ситуации. В первом случае два ряда находятся в одинаковом положении по отношению друг к другу, как, например, два входа на рис. 8.1.

Рис. 8.2. Синфазный и сдвинутый по фазе токи на выходе турбогенератора.

В этом случае могут быть двумя коррелированными переменными управления, взаимодействие которых мы хотим изучить. Пример пары временных рядов, попадающих в эту категорию, приведен на рис. 8.2,

где приведены записи синфазного и сдвинутого по фазе входных токов турбогенератора.

Во втором случае два временных ряда причинно связаны, например вход на рис. 8.1 и зависящий от него выход . В такой ситуации обычно требуется оценить свойства системы в такой форме, чтобы было удобно предсказывать выход по входу. Пример пары временных рядов такого типа приведен на рис. 8.3, где показана скорость впуска газа и концентрация двуокиси углерода на выходе газовой печи.

Рис. 8.3. Сигналы на входе и выходе газовой печи.

Видно, что выход запаздывает по отношению ко входу из-за того, что для доставки газа к реактору требуется некоторое время.

Взаимные корреляционные функции сигналов

Взаимная корреляционная функция (ВКФ) разных сигналов (cross-correlation function, CCF) описывает как степень сходства формы двух сигналов, так и их взаимное расположение друг относительно друга по координате (независимой переменной). Обобщая формулу (6.1) автокорреляционной функции на два различных сигнала s(t) и u(t), получаем следующее скалярное произведение сигналов:

B su (t) =s(t) u(t+t) dt. (6.14)

Взаимная корреляция сигналов характеризует определенную корреляцию явлений и физических процессов, отображаемых данными сигналами, и может служить мерой “устойчивости” данной взаимосвязи при раздельной обработке сигналов в различных устройствах. Для конечных по энергии сигналов ВКФ также конечна, при этом:

|B su (t)| £ ||s(t)||×||u(t)||,

что следует из неравенства Коши-Буняковского и независимости норм сигналов от сдвига по координатам.

При замене переменной t = t-t в формуле (6.2.1), получаем:

B su (t) =s(t-t) u(t) dt =u(t) s(t-t) dt = B us (-t).

Отсюда следует, что для ВКФ не выполняется условие четности, B su (t) ¹ B su (-t), и значения ВКФ не обязаны иметь максимум при t = 0.

Это можно наглядно видеть на рис. 6.6, где заданы два одинаковых сигнала с центрами на точках 0.5 и 1.5. Вычисление по формуле (6.14) с постепенным увеличением значений t означает последовательные сдвиги сигнала s2(t) влево по оси времени (для каждого значения s1(t) для подынтегрального умножения берутся значения s2(t+t)). При t=0 сигналы ортогональны и значение B 12 (t)=0. Максимум В 12 (t) будет наблюдаться при сдвиге сигнала s2(t) влево на значение t=1, при котором происходит полное совмещение сигналов s1(t) и s2(t+t).

Рис. 6.6. Сигналы и ВКФ

Одни и те же значения ВКФ по формулам (6.14) и (6.14") наблюдаются при одном и том же взаимном положении сигналов: при сдвиге на интервал t сигнала u(t) относительно s(t) вправо по оси ординат и сигнала s(t) относительно сигнала u(t) влево, т.е. B su (t) = B us (-t).

На рис. 6.7 приведены примеры ВКФ для прямоугольного сигнала s(t) и двух одинаковых треугольных сигналов u(t) и v(t). Все сигналы имеют одинаковую длительность Т, при этом сигнал v(t) сдвинут вперед на интервал Т/2.

Рис. 6.7. Взаимноковариационные функции сигналов

Сигналы s(t) и u(t) одинаковы по временному расположению и площадь "перекрытия" сигналов максимальна при t=0, что и фиксируется функцией B su . Вместе с тем функция B su резко асимметрична, так как при асимметричной форме сигнала u(t) для симметричной формы s(t) (относительно центра сигналов) площадь "перекрытия" сигналов изменяется по разному в зависимости от направления сдвига (знака t при увеличения значения t от нуля). При смещении исходного положения сигнала u(t) влево по оси ординат (на опережение сигнала s(t) - сигнал v(t)) форма ВКФ остается без изменения и сдвигается вправо на такое же значение величины сдвига – функция B sv на рис. 6.7. Если поменять местами выражения функций в (6.14), то новая функция B vs будет зеркально повернутой относительно t=0 функцией B sv .

С учетом этих особенностей полное ВКФ вычисляется, как правило, отдельно для положительных и отрицательных запаздываний:

B su (t) =s(t) u(t+t) dt. B us (t) =u(t) s(t+t) dt. (6.14")

Взаимная корреляционная функция (ВКФ) разных сигналов (cross-correlation function, CCF) описывает как степень сходства формы двух сигналов, так и их взаимное расположение друг относительно друга по координате (независимой переменной). Обобщая формулу (6.1.1) автокорреляционной функции на два различных сигнала s(t) и u(t), получаем следующее скалярное произведение сигналов:

B su () =s(t) u(t+) dt. (6.2.1)

Взаимная корреляция сигналов характеризует определенную корреляцию явлений и физических процессов, отображаемых данными сигналами, и может служить мерой “устойчивости” данной взаимосвязи при раздельной обработке сигналов в различных устройствах. Для конечных по энергии сигналов ВКФ также конечна, при этом:

|B su ()|  ||s(t)||||u(t)||,

что следует из неравенства Коши-Буняковского и независимости норм сигналов от сдвига по координатам.

При замене переменной t = t- в формуле (6.2.1), получаем:

B su () =s(t-) u(t) dt = u(t) s(t-) dt = B us (-).

Отсюда следует, что для ВКФ не выполняется условие четности, B su ()  B su (-), и значения ВКФ не обязаны иметь максимум при  = 0.

Рис. 6.2.1. Сигналы и ВКФ.

Одни и те же значения ВКФ по формулам (6.2.1) и (6.2.1") наблюдаются при одном и том же взаимном положении сигналов: при сдвиге на интервал  сигнала u(t) относительно s(t) вправо по оси ординат и сигнала s(t) относительно сигнала u(t) влево, т.е. B su () = B us (-

Рис. 6.2.2. Взаимноковариационные функции сигналов.

Сигналы s(t) и u(t) одинаковы по временному расположению и площадь "перекрытия" сигналов максимальна при =0, что и фиксируется функцией B su . Вместе с тем функция B su резко асимметрична, так как при асимметричной форме сигнала u(t) для симметричной формы s(t) (относительно центра сигналов) площадь "перекрытия" сигналов изменяется по разному в зависимости от направления сдвига (знака  при увеличения значения  от нуля). При смещении исходного положения сигнала u(t) влево по оси ординат (на опережение сигнала s(t) - сигнал v(t)) форма ВКФ остается без изменения и сдвигается вправо на такое же значение величины сдвига – функция B sv на рис. 6.2.2. Если поменять местами выражения функций в (6.2.1), то новая функция B vs будет зеркально повернутой относительно =0 функцией B sv .

С учетом этих особенностей полное ВКФ вычисляется, как правило, отдельно для положительных и отрицательных запаздываний:

B su () =s(t) u(t+) dt. B us () =u(t) s(t+) dt. (6.2.1")

Взаимная корреляция зашумленных сигналов . Для двух зашумленных сигналов u(t) = s1(t)+q1(t) и v(t) = s2(t)+q2(t), применяя методику вывода формул (6.1.13) с заменой копии сигнала s(t) на сигнал s2(t), нетрудно вывести формулу взаимной корреляции в следующем виде:

B uv () = B s1s2 () + B s1q2 () + B q1s2 () + B q1q2 (). (6.2.2)

Последние три члена в правой части (6.2.2) затухают до нуля при увеличении . При больших интервалах задания сигналов выражение может быть записано в следующей форме:

B uv () = B s 1 s 2 () +
+
+
. (6.2.3)

При нулевых средних значениях шумов и статистической независимости от сигналов имеет место:

B uv () → B s 1 s 2 ().

ВКФ дискретных сигналов. Все свойства ВКФ аналоговых сигналов действительны и для ВКФ дискретных сигналов, при этом для них действительны и особенности дискретных сигналов, изложенные выше для дискретных АКФ (формулы 6.1.9-6.1.12). В частности, при t = const =1 для сигналов x(k) и y(k) с числом отсчетов К:

B xy (n) =
x k y k-n . (6.2.4)

При нормировании в единицах мощности:

B xy (n) = x k y k-n 
. (6.2.5)

Оценка периодических сигналов в шуме . Зашумленный сигнал можно оценить по взаимной корреляции с "эталонным" сигналом методом проб и ошибок с настройкой функции взаимной корреляции до максимального значения.

Для сигнала u(k)=s(k)+q(k) при статистической независимости шума и → 0 функция взаимной корреляции (6.2.2) с шаблоном сигнала p(k) при q2(k)=0 принимает вид:

B up (k) = B sp (k) + B qp (k) = B sp (k) + .

А поскольку → 0 при увеличении N, тоB up (k) → B sp (k). Очевидно, что функция B up (k) будет иметь максимум, когда p(k) = s(k). Меняя форму шаблона p(k) и добиваясь максимизации функции B up (k), можно получить оценку s(k) в виде оптимальной формы p(k).

Функция взаимных корреляционных коэффициентов (ВКФ) является количественным показателем степени сходства сигналов s(t) и u(t). Аналогично функции автокорреляционных коэффициентов, она вычисляется через центрированные значения функций (для вычисления взаимной ковариации достаточно центрировать только одну из функций), и нормируется на произведение значений стандартов функций s(t) и v(t):

 su () = C su ()/ s  v . (6.2.6)

Интервал изменения значений корреляционных коэффициентов при сдвигах  может изменяться от –1 (полная обратная корреляция) до 1 (полное сходство или стопроцентная корреляция). При сдвигах , на которых наблюдаются нулевые значения  su (), сигналы независимы друг от друга (некоррелированны). Коэффициент взаимной корреляции позволяет устанавливать наличие связи между сигналами вне зависимости от физических свойств сигналов и их величины.

При вычислении ВКФ зашумленных дискретных сигналов ограниченной длины с использованием формулы (6.2.4) имеется вероятность появления значений  su (n)| > 1.

Для периодических сигналов понятие ВКФ обычно не применяется, за исключением сигналов с одинаковым периодом, например, сигналов входа и выхода при изучении характеристик систем.

Взаимнокорреляционная функция - стандартный метод оценки степени корреляции двух последовательностей. Она часто используется для поиска в длинной последовательности более короткой заранее известной. Рассмотрим два ряда f и g. Взаимная корреляция определяется по формуле:

$(f\backslash star\; g)\_i\; \backslash \; \backslash stackrel\{\backslash mathrm\{def\}\}\{=\}\backslash \; \backslash sum\_j\; f^*\_j\backslash ,g\_\{i+j\}$,

где $i$ - сдвиг между последовательностями относительно друг друга, а верхний индекс в виде звёздочки означает комплексное сопряжение . В общем случае, для непрерывных функций f (t ) и g (t ) взаимная корреляция определяется как

$(f\; \backslash star\; g)(t)\backslash \; \backslash stackrel\{\backslash mathrm\{def\}\}\{=\}\; \backslash int\_\{-\backslash infty\}^\{\backslash infty\}\; f^*(\backslash tau)\backslash \; g(t+\backslash tau)\backslash ,d\backslash tau,$

Если $X$ и $Y$ - два независимых случайных числа с функциями распределения вероятностей соответственно f и g , тогда взаимная корреляция f $\backslash star$ g соответствует распределению вероятностей выражения $-X\; +\; Y$. Напротив, свёртка f $*$ g соответствует распределению вероятностей суммы $X\; +\; Y$.

Свойства

Взаимная корреляция и свёртка взаимосвязанны:

$f(t)\backslash star\; g(t)\; =\; f^*(-t)*g(t)$

поэтому, если функции f и g чётны, то

$(f\backslash star\; g)\; =\; f*g$

Также: $(f\backslash star\; g)\backslash star(f\backslash star\; g)=(f\backslash star\; f)\backslash star\; (g\backslash star\; g)$

См. также.

Напишите отзыв о статье "Взаимнокорреляционная функция"

Ссылки

• функция в MATLAB

Отрывок, характеризующий Взаимнокорреляционная функция