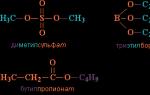
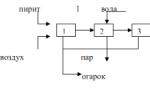
Пример решения эмпирическая функция распределения. Эмпирическая функция распределения, свойства. Графическое изображение рядов распределения

Определение эмпирической функции распределения

Пусть $X$ -- случайная величина. $F(x)$ - функция распределения данной случайной величины. Будем проводить в одних и тех же независимых друг от друга условий $n$ опытов над данной случайной величиной. При этом получим последовательность значений $x_1,\ x_2\ $, ... ,$\ x_n$, которая и называется выборкой.

Определение 1

Каждое значение $x_i$ ($i=1,2\ $, ... ,$ \ n$) называется вариантой.

Одной из оценок теоретической функции распределения является эмпирическая функция распределения.

Определение 3

Эмпирической функцией распределения $F_n(x)$ называется функция, которая определяет для каждого значения $x$ относительную частоту события $X \

где $n_x$ - число вариант, меньших $x$, $n$ -- объем выборки.

Отличие эмпирической функции от теоретической состоит том, что теоретическая функция определяет вероятность события $X

Свойства эмпирической функции распределения

Рассмотрим теперь несколько основных свойств функции распределения.

Область значений функции $F_n\left(x\right)$ -- отрезок $$.

$F_n\left(x\right)$ неубывающая функция.

$F_n\left(x\right)$ непрерывная слева функция.

$F_n\left(x\right)$ кусочно-постоянная функция и возрастает только в точках значений случайной величины $X$

Пусть $X_1$ -- наименьшая, а $X_n$ -- наибольшая варианта. Тогда $F_n\left(x\right)=0$ при ${x\le X}_1$и $F_n\left(x\right)=1$ при $x\ge X_n$.

Введем теорему, которая связывает между собой теоретическую и эмпирическую функции.

Теорема 1

Пусть $F_n\left(x\right)$ -- эмпирическая функция распределения, а $F\left(x\right)$ -- теоретическая функция распределения генеральной выборки. Тогда выполняется равенство:

\[{\mathop{lim}_{n\to \infty } {|F}_n\left(x\right)-F\left(x\right)|=0\ }\]

Примеры задач на нахождение эмпирической функции распределения

Пример 1

Пусть распределение выборки имеет следующие данные, записанные с помощью таблицы:

Рисунок 1.

Найти объем выборки, составить эмпирическую функцию распределения и построить её график.

Объем выборки: $n=5+10+15+20=50$.

По свойству 5, имеем, что при $x\le 1$ $F_n\left(x\right)=0$, а при $x>4$ $F_n\left(x\right)=1$.

Значение $x

Значение $x

Значение $x

Таким образом, получаем:

Рисунок 2.

Рисунок 3.

Пример 2

Из городов центральной части России случайным образом выбрано 20 городов, для которых получены следующие данные по стоимости проезда в общественном транспорте: 14, 15, 12, 12, 13, 15, 15, 13, 15, 12, 15, 14, 15, 13, 13, 12, 12, 15, 14, 14.

Составить эмпирическую функцию распределения данной выборки и построить её график.

Запишем значения выборки в порядке возрастания и посчитаем частоту каждого значения. Получаем следующую таблицу:

Рисунок 4.

Объем выборки: $n=20$.

По свойству 5, имеем, что при $x\le 12$ $F_n\left(x\right)=0$, а при $x>15$ $F_n\left(x\right)=1$.

Значение $x

Значение $x

Значение $x

Таким образом, получаем:

Рисунок 5.

Построим график эмпирического распределения:

Рисунок 6.

Оригинальность: $92,12\%$.

Как известно, закон распределения случайной величины можно задавать различными способами. Дискретную случайную величину можно задать с помощью ряда распределения или интегральной функции, а непрерывную случайную величину – с помощью или интегральной, или дифференциальной функции. Рассмотрим выборочные аналоги этих двух функций.

Пусть имеется выборочная совокупность значений некоторой случайной величины объемаи каждому варианту из этой совокупности поставлена в соответствие его частость. Пусть далее,– некоторое действительное число, а– число выборочных значений случайной величины
, меньших.Тогда числоявляется частостью наблюдаемых в выборке значений величиныX , меньших , т.е. частостью появления события
. При измененииx в общем случае будет изменяться и величина . Это означает, что относительная частотаявляется функцией аргумента. А так как эта функция находится по выборочным данным, полученным в результате опытов, то ее называют выборочной илиэмпирической .

Определение 10.15. Эмпирической функцией распределения (функцией распределения выборки) называют функцию
, определяющую для каждого значенияx относительную частоту события
.

(10.19)

В отличие от эмпирической функции распределения выборки функцию распределения F (x ) генеральной совокупности называют теоретической функцией распределения . Различие между ними состоит в том, что теоретическая функция F (x ) определяет вероятность события
, а эмпирическая – относительную частоту этого же события. Из теоремы Бернулли следует

,
(10.20)

т.е. при больших вероятность
и относительная частота события
, т.е.
мало отличаются одно от другого. Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.

Функция
и
обладают одинаковыми свойствами. Это вытекает из определения функции.

Свойства
:

Пример 10.4. Построить эмпирическую функцию по данному распределению выборки:

Решение: Найдем объем выборки n = 12+18+30=60. Наименьшая варианта
, следовательно,
при
. Значение
, а именно
наблюдалось 12 раз, следовательно:

=
при
.

Значение x < 10, а именно
и
наблюдались 12+18=30 раз, следовательно,
=
при
. При

.

Искомая эмпирическая функция распределения:

=

График
представлен на рис. 10.2

Р
ис. 10.2

Контрольные вопросы

1. Какие основные задачи решает математическая статистика? 2. Генеральная и выборочная совокупность? 3. Дайте определение объема выборки. 4. Какие выборки называются репрезентативными? 5. Ошибки репрезентативности. 6. Основные способы образования выборки. 7. Понятия частоты, относительной частоты. 8. Понятие статистического ряда. 9. Запишите формулу Стэрджеса. 10. Сформулируйте понятия размаха выборки, медианы и моды. 11. Полигон частот, гистограмма. 12. Понятие точечной оценки выборочной совокупности. 13. Смещенная и несмещенная точечная оценка. 14. Сформулируйте понятие выборочной средней. 15. Сформулируйте понятие выборочной дисперсии. 16. Сформулируйте понятие выборочного среднеквадратического отклонения. 17. Сформулируйте понятие выборочного коэффициента вариации. 18. Сформулируйте понятие выборочной средней геометрической.

Пусть X 1 , X 2 , ..., X n -- выборка объема п из генеральной совокупности с функцией распределения F (x ). Если расположить выборочные данные в порядке неубывания, то полученный ряд называется вариационным рядом: X (1) , X (2) , ..., X (n )

Пример 1. Если выборка объема 4 следующая: 4, -2, 3, 1, то вариационный ряд выглядит так: -2, 1, 3, 4.

Определение 1. Эмпирической называется функция распределения F (x ) дискретной случайной величины, у которой таблица распределения имеет следующий вид:

Как показано в 2.2.1 функция распределения дискретной случайной величины

имеет следующий вид:

Другими словами F n (x ) = v/n, где v --число тех выборочных значений X i , которые меньше х.

Как видно из графика, функция F n (x ) ступенчатая и имеет разрывы в точках X (i) и величина скачка равна 1/n , если совпадающих друг с другом значений X i , нет. Если же k значений X (i) совпадают, то величина скачка в этой точке равна k/n .

Представляет интерес предельное поведение F n (x ) при п .

Теорема 1. Пусть X 1 , X 2 , ..., X n -- выборка объема п из генеральной совокупности функцией распределения F (x ). Тогда при п со для любого х 1 справедливо

F n (x ) P F (x ),

или, другими словами, для любого > 0,

Доказательство. Пусть

такие дискретные случайные величины, что Р(i == 0) = q и P(i = 1) = р, i = 1. 2..... п. Легко видеть, что

Тогда по закону больших чисел (см. 2.7.2) для эмпирической функции распределения F n (x ) = 1/n n i=1 i при п получим

F n (x ) P F (x ),

Прежде чем сформулировать еще одну теорему, приведем следующее определение.

Определение 2. Последовательность случайных величин 1 , 2 , …, n , … сходится к с вероятностью 1 {единица) {или почти наверное), если выполняется следующее равенство

Теперь сформулируем (без доказательства, его можно найти в ) следующую теорему.

Теорема 2 (Гливенко - Кантелли). В условиях предыдущей теоремы справедливо

Эти результаты показывают, что при больших п эмпирическая функция распределения дает хорошее приближение для теоретической функции распределения F (x ).

Выборки объема п из генеральной совокупности с непрерывным распределением F (x ) на практике часто подвергаются группировке. В этом случае указываются не выборочные значения, а число выборочных значений, попавших в интервалы некоторого определенного разбиения генеральной совокупности (разбиения множества возможных значений случайной величины, имеющей функцию распределения F (x ) ). Как правило, интервалы берутся одинаковой длины, скажем h. Если обозначить через n i число выборочных значений, попавших в i - интервал, то этот интервал принимается за основание прямоугольника высоты n i /nh. Получающаяся при этом фигура называется гистограммой выборки. Площадь каждого прямоугольника гистограммы равна частоте n i /n соответствующей группы. При больших п эта площадь будет приблизительно равна вероятности попасть в соответствующий интервал, т.е. будет приблизительно равна интегралу от плотности распределения р(t ), вычисленному по данному интервалу. Таким образом, верхняя часть контура гистограммы дает хорошее приближение для плотности распределения.

Пример 2. Испытывалась чувствительность 1-го канала п = 40 телевизоров. Данные испытаний указаны в следующей таблице, где в первой строке даны интервалы чувствительности в микровольтах, во второй - число телевизоров, чувствительность которых оказалась данном интервале:

Здесь длина интервала h = 50. Построим гистограмму.

Вариационный ряд. Полигон и гистограмма.

Ряд распределения - представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.

В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения:

§ Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными .

Вариационный ряд распределения состоит из двух столбцов:

В первом столбце приводятся количественные значения варьирующегося признака, которые называются вариантами и обозначаются . Дискретная варианта - выражается целым числом. Интервальная варианта находится в пределах от и до. В зависимости от типа варианты можно построить дискретный или интервальный вариационный ряд.
Во втором столбце содержится количество конкретных вариант , выраженное через частоты или частости:

Частоты - это абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака, которые обозначают . Сумма всех частот равна должна быть равна численности единиц всей совокупности.

Частости () - это частоты выраженные в процентах к итогу. Сумма всех частостей выраженных в процентах должна быть равна 100% в долях единице.

Графическое изображение рядов распределения

Наглядно ряды распределения представляются при помощи графических изображений.

Ряды распределения изображаются в виде:

§ Полигона

§ Гистограммы

§ Кумуляты

Полигон

При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) - частоты или частости.

1. Полигон на рис. 6.1 построен по данным микропереписи населения России в 1994 г.

Гистограмма

Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).

На рис. 6.2. изображена гистограмма распределения населения России в 1997 г. по возрастным группам.

Рис.1. Распределение населения России по возрастным группам

Эмпирическая функция распределения, свойства.

Пусть известно статистическое распределение частот количественного признака X. Обозначим через число наблюдений, при которых наблюдалось значение признака, меньшее x и через n – общее число наблюдений. Очевидно, относительная частота события X

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения x относительную частоту события X

В отличие от эмпирической функции распределения выборки, функцию распределения генеральной совокупности называют теоретической функцией распределения. Различие между этими функциями состоит в том, что теоретическая функция определяет вероятность события X

При росте n относительная частота события X

Основные свойства

Пусть зафиксирован элементарный исход . Тогда является функцией распределения дискретного распределения, задаваемого следующейфункцией вероятности:

где , а - количество элементов выборки, равных . В частности, если все элементы выборки различны, то .

Математическое ожидание этого распределения имеет вид:

.

Таким образом выборочное среднее - это теоретическое среднее выборочного распределения.

Аналогично, выборочная дисперсия - это теоретическая дисперсия выборочного распределения.

Случайная величина имеет биномиальное распределение:

Выборочная функция распределения является несмещённой оценкой функции распределения :

.

Дисперсия выборочной функции распределения имеет вид:

.

Согласно усиленному закону больших чисел, выборочная функция распределения сходится почти наверное к теоретической функции распределения:

почти наверное при .

Выборочная функция распределения является асимптотически нормальной оценкой теоретической функции распределения. Если , то

По распределению при .

Пусть изучается некоторый количественный признак? генеральной совокупности, и предположим, что при любом объеме выборки известно распределение частот этого признака. Зафиксировав объем выборки равным п, обозначим через п х число вариант, меньших чем х. Тогда нетрудно видеть, что отношение njn выражает относительную частоту события (?

Это отношение зависит от фиксированного числа х и, следовательно, является некоторой функцией этой величины х. Обозначим ее через F*(x).

Определение 1.10. Функция F* (х) = -, выражающая относительную

частоту события (? эмпирической функцией

распределения (функцией распределения выборки или статистической функцией распределения ).

Таким образом, по определению

Напомним, что функция распределения признака ?, генеральной совокупности определяется как вероятность события (?

и в отличие от эмпирической функции распределения называется теоретической функцией распределения. Так как эмпирическая функция распределения - вероятность этого же события, то согласно теореме Бернулли (см. п. 5.4, ) при большом объеме выборки они мало отличаются друг от друга в том смысле, что

где е - любое сколь угодно малое положительное число.

Соотношение (1.2) показывает, что если теоретическая функция распределения неизвестна, то найденную из выборки эмпирическую функцию распределения можно использовать в качестве ее выборочной оценки. Из формулы (1.2) одновременно следует, что эта оценка и состоятельна (см. определение 2.4).

Замечание 1.6. Отношение пJn можно интерпретировать еще как долю тех членов выборки, которые лежат левее фиксированного числа х. Обозначим ее через со^.Следовательно,

А теперь рассмотрим пример построения эмпирической функции распределения для дискретной выборки.

Пример 1.2. Известно распределение выборки (табл. 1.7).

Табл и ца 1.7

Построить ее эмпирическую функцию распределения.

Сначала найдем объем выборки:

Варианта х х - наименьшая. Поэтому п х = 0 и F*(x) = 0 при х % 3, то п з = 6, т.е. левее точки х = 3 находятся шесть значений выборки. Следовательно, F* (3) = - = 0,12. Левее х = 5 располо-

жены п х=5 = 6 + 9= 15 вариант выборки. Поэтому F n (5) = - = 0,3. Так

как п х=1 = 6 + 9 + 18 = 33, то F n (7) = - = 0,66. Аналогично находим

33 + 12 = 45. Поэтому F* (9) = ^ = 0,9.

Варианта х 5 = 9 - наибольшая. Следовательно, при х > 9 вся выборка лежит левее этой точки х. Поэтому п х>9 = 50 и F* (х) = -= 1 при х > 9. 50

Таким образом, из вычислений, проведенных выше, следует, что искомая эмпирическая функция однозначно определена на всей вещественной оси, кусочно-постоянна и имеет вид

График этой функции представляет ступенчатую фигуру и изображен на рис. 1.6. ?

Что касается вопроса о построении эмпирической функции для непрерывных выборок, то эта задача решается, вообще говоря, далеко не однозначно. Это связано с тем обстоятельством, что значения эмпирической функции можно найти однозначно только в концевых точках частичных интервалов, на которые разбит основной интервал, содержащий выборочную совокупность. А во внутренних точках частичных интервалов она не определена. В этих точках она доопределяется либо кусочно-постоянной функцией (см. предыдущий пример), либо некоторой возрастающей непрерывной функцией, например линейной функцией, т.е. для построения эмпирической функции распределения используется линейная аппроксимация.

Пример 1.3. По данным таблицы 1.3 найти эмпирическую функцию распределения работников предприятия по стажу работы.

Для определенности предположим, что рассматриваемые частичные промежутки слева замкнуты, а справа открыты, т.е. они содержат только свои левые концы. Пусть х = 2. Тогда событие п 2 = 0 и F*(2) = 0. Если же х е (2; 6), то в этой точке величина п х уже не определена и вместе с ней не определено и значение эмпирической функции. Например, если х = 3, то из условия задачи нельзя определить число рабочих, имеющих стаж работы менее трех лет, т.е. нельзя найти частоту п х и, следовательно, F*(x).

Далее, рассуждая аналогично, убеждаемся, что искомая функция F*(x) принимает конкретные значения в левых концевых точках частичных интервалов, например: «6) = 4/100 = 0,04; «10) = 0,12; «14) = 0,24; «18) = 0,59; F*(22) = 0,78; «26) = 0,90”; «30) = 1, но она не определена во внутренних точках частичных интервалов. Для окончательного решения задачи искомую функцию во внутренних точках частичных интервалов доопределяют либо кусочно-постоянной функцией (рис. 1.7), либо некоторой непрерывной возрастающей функцией (рис. 1.8, где искомая эмпирическая функция доопределена линейной функцией). ?